题目内容
4．
已知：如图，在?ABCD中，M、N分别是AB、CD的中点，AN与DM相交于点P，BN与CM相交于点Q．求证：四边形PMQN是平行四边形．
分析 由平行四边形的性质得出AB=DC，AB∥CD，证出四边形DMBN是平行四边形，得出对边平行PM∥NQ，同理：PN∥MQ，即可得出结论．
解答 证明：∵四边形ABCD是平行四边形，
∴AB=DC，AB∥CD，
∵M、N分别是AB、CD的中点，
∴DN=CN=$\frac{1}{2}$DC，AM=BM=$\frac{1}{2}$AB，
∴DN∥BM，DN=BM，
∴四边形DMBN是平行四边形，
∴PM∥NQ，
同理：PN∥MQ，
∴四边形PMQN是平行四边形．
点评 本题考查了平行四边形的性质和平行四边形的判定的综合运用；证明四边形DMEN是平行四边形是解决问题的关键解题的关键．
练习册系列答案
相关题目
15．抛物线y=-$\frac{1}{2}$（x-2）2+1的顶点坐标是（ ）
| A． | （-2，-1） | B． | （-2，1） | C． | （2，-1） | D． | （2，1） |
如图，直线a、b被直线c所截，且a∥b．若∠1=35°，则∠2=145°．
19．
如图，已知直线AB∥CD，∠C=120°，∠A=45°，那么∠E的大小为（ ）
如图，已知直线AB∥CD，∠C=120°，∠A=45°，那么∠E的大小为（ ）| A． | 70° | B． | 75° | C． | 80° | D． | 85° |
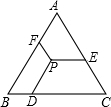如图所示，△ABC是等边三角形，P是其内任意一点，PD∥AB，PE∥BC，PF∥AC，若△ABC的周长为24，则PD+PE+PF=8．