题目内容
20.已知x为实数,且$\frac{3}{{x}^{2}+x}$-(x2+x)=2,则x2+x的值为( )| A. | 0 | B. | 1 | C. | 2 | D. | x2 |
分析 根据换元法,可得u=x2+x,根据解分式方程,可得答案.
解答 解:设u=x2+x,得
$\frac{3}{μ}$-μ=2.
3-u2=2u,
解得u1=-3,u2=1.
当x2+x=-3时,即x2+x+3=0,△=12-4×3=-11<0,故不符合题意.
故x2+x的值为1.
故选:B.
点评 本题考查了用换元法解方程,解题关键是能准确的找出可用替换的代数式x2+x,再用字母u代替解方程.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
11.下列说法正确的是( )
| A. | 每个定理都有逆定理 | B. | 每个命题都有逆命题 | ||
| C. | 假命题没有逆命题 | D. | 真命题的逆命题是真命题 |
5.《九章算术》商功章有题:一圆柱形谷仓,高1丈3尺3$\frac{1}{3}$寸,容纳米2000斛(1丈=10尺,1尺=10寸,斛为容积单位,1斛≈1.62立方尺,π=3),则圆柱底周长约为(注:圆柱体的体积=底面积×高)( )
| A. | 1丈3尺 | B. | 5丈4尺 | C. | 9丈2尺 | D. | 48丈6尺 |
12.给出四个数0,$\sqrt{2}$,$\frac{1}{3}$,-1,其中最小的数是( )
| A. | 0 | B. | $\sqrt{2}$ | C. | $\frac{1}{3}$ | D. | -1 |
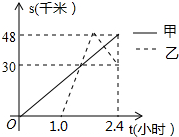 甲、乙两车分别从A地将一批物品运往B地,再返回A地,如图表示两车离A地的距离s(千米)随时间t(小时)变化的图象,已知乙车到达B地后以30千米/小时的速度返回,则下列说法正确的有( )
甲、乙两车分别从A地将一批物品运往B地,再返回A地,如图表示两车离A地的距离s(千米)随时间t(小时)变化的图象,已知乙车到达B地后以30千米/小时的速度返回,则下列说法正确的有( )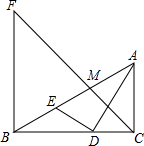 如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F,BD=2,CD=1.下列结论:①∠AED=∠ADC;②$\frac{DE}{DA}$=$\frac{1}{2}$;③BF=2AC;④BE=DE,其中正确的有①③④(把所有正确结论的序号都填在横线上).
如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F,BD=2,CD=1.下列结论:①∠AED=∠ADC;②$\frac{DE}{DA}$=$\frac{1}{2}$;③BF=2AC;④BE=DE,其中正确的有①③④(把所有正确结论的序号都填在横线上). 某射击小组进行射击练习,教练将该小组成员的某次射击成绩绘制成统计图(如图),则这组成绩的众数是7.
某射击小组进行射击练习,教练将该小组成员的某次射击成绩绘制成统计图(如图),则这组成绩的众数是7.