题目内容
9.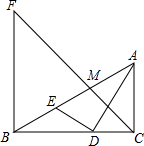 如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F,BD=2,CD=1.下列结论:①∠AED=∠ADC;②$\frac{DE}{DA}$=$\frac{1}{2}$;③BF=2AC;④BE=DE,其中正确的有①③④(把所有正确结论的序号都填在横线上).
如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F,BD=2,CD=1.下列结论:①∠AED=∠ADC;②$\frac{DE}{DA}$=$\frac{1}{2}$;③BF=2AC;④BE=DE,其中正确的有①③④(把所有正确结论的序号都填在横线上).
分析 ①根据已知条件得到∠AED=90°-∠EAD,∠ADC=90°-∠DAC,即可得到结论;
②易证△ADE∽△ACD,根据相似三角形的性质得到DE:DA=DC:AC=1:AC,AC不一定等于2;
③连接DM,可证DM∥BF∥AC,得FM:MC=BD:DC=4:3;易证△FMB∽△CMA,得比例线段求解;
④BE=DE成立.由④可知BM:MA=BF:AC=2:1,而BD:DC=2:1,可知DM∥AC,DM⊥BC,利用直角三角形斜边上的中线的性质判断.
解答 解:①∠AED=90°-∠EAD,∠ADC=90°-∠DAC,
∵∠EAD=∠DAC,
∴∠AED=∠ADC.
故本选项正确;
②∵∠EAD=∠DAC,∠ADE=∠ACD=90°,
∴△ADE∽△ACD,得DE:DA=DC:AC=1:AC,但AC的值未知,
故不一定正确;
③连接DM.
在Rt△ADE中,MD为斜边AE的中线,则DM=MA.
∴∠MDA=∠MAD=∠DAC,
∴DM∥BF∥AC,
由DM∥BF得FM:MC=BD:DC=2:1;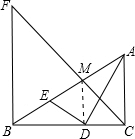
由BF∥AC得△FMB∽△CMA,有BF:AC=FM:MC=2:1,
∴BF=2AC.
故本选项正确;
④由③可知BM:MA=BF:AC=2:1
∵BD:DC=2:1,∴DM∥AC,DM⊥BC,
∴∠MDA=∠DAC=∠DAM,而∠ADE=90°,
∴DM=MA=ME,在Rt△BDM中,由BM=2AM可知BE=EM,
∴ED=BE.故④正确.
故答案为:①③④.
点评 此题重点考查相似三角形的判定和性质,解题的关键是注意题目中相等线段的替换,此题综合性强,有一定难度.

练习册系列答案
相关题目
19.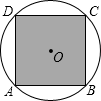 如图,正方形ABCD内接于⊙O,⊙O的直径为$\sqrt{2}$分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )
如图,正方形ABCD内接于⊙O,⊙O的直径为$\sqrt{2}$分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )
 如图,正方形ABCD内接于⊙O,⊙O的直径为$\sqrt{2}$分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )
如图,正方形ABCD内接于⊙O,⊙O的直径为$\sqrt{2}$分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )| A. | $\frac{2}{π}$ | B. | $\frac{π}{2}$ | C. | $\frac{1}{2π}$ | D. | $\sqrt{2}π$ |
14.下列运算正确的是( )
| A. | -$\sqrt{(-13)^{2}}$=13 | B. | $\sqrt{(-6)^{2}}$=-6 | C. | -$\sqrt{25}$=-5 | D. | $\sqrt{9}$=±3 |
 -(a+2b)2=a2-4b2
-(a+2b)2=a2-4b2