题目内容
5. 如图,△ABC中,∠C,∠B的平分线相交于O,过O作AO的垂线与边AB、AC分别交于D、E,求证:△BDO∽△BOC∽△OEC.
如图,△ABC中,∠C,∠B的平分线相交于O,过O作AO的垂线与边AB、AC分别交于D、E,求证:△BDO∽△BOC∽△OEC.
分析 由角平分线的交点得出∠OBD=∠OBC=$\frac{1}{2}$∠ABC,∠OCE=∠OCB=$\frac{1}{2}$∠ACB,∠OA平分∠BAC,由三角形的外角性质得出∠ODB=∠OAD+∠AOD=$\frac{1}{2}$∠BAC+90°,由三角形内角和定理得出∠BOC=$\frac{1}{2}$∠BAC+90°,证出△BDO∽△BOC,同理:△BOC∽△OEC,即可得出结论.
解答 证明:∵∠C,∠B的平分线相交于O,
∴∠OBD=∠OBC=$\frac{1}{2}$∠ABC,∠OCE=∠OCB=$\frac{1}{2}$∠ACB,∠OA平分∠BAC,
∴∠OAD=∠OAE=$\frac{1}{2}$∠BAC,
∵AO⊥DE,
∴∠AOD=∠AOE=90°,
∴∠ODB=∠OAD+∠AOD=$\frac{1}{2}$∠BAC+90°,
∵∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°-∠BAC)=90°-$\frac{1}{2}$∠BAC,
∴∠BOC=180°-(∠OBC+∠OCB)=$\frac{1}{2}$∠BAC+90°,
∴△BDO∽△BOC,
同理:△BOC∽△OEC,
∴△BDO∽△BOC∽△OEC.
点评 本题考查了角平分线的交点的性质、相似三角形的判定与性质、三角形的外角性质;熟练掌握相似三角形的判定方法,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
17.若x是有理数,则x2+1一定是( )
| A. | 等于1 | B. | 大于1 | C. | 不小于1 | D. | 不大于1 |
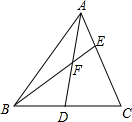 在△ABC中,D是边BC的中点,F是AD的中点,求AE:EC的值.
在△ABC中,D是边BC的中点,F是AD的中点,求AE:EC的值.