题目内容
14.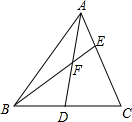 在△ABC中,D是边BC的中点,F是AD的中点,求AE:EC的值.
在△ABC中,D是边BC的中点,F是AD的中点,求AE:EC的值.
分析 过点D作DM∥AC交DE于点M,易证△AEF≌△DMF,所以DM=AE,由三角形中位线定理可知CE=2DM,进而可求出AE:EC的值.
解答 解:过点D作DM∥AC交DE于点M,
∴∠AEF=∠DMF,∠FAE=∠FDM,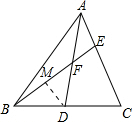
∵F是AD的中点,
∴AF=DF,
在△AEF和△DMF中
$\left\{\begin{array}{l}{∠EAF=∠MDF}\\{∠AEF=∠DMF}\\{AF=DF}\end{array}\right.$,
∴△AEF≌△DMF(AAS),
∴DM=AE,
∴D是边BC的中点,DM∥AC,
∴DM=$\frac{1}{2}$CE,
∴AE:EC=DM:CE=1:2.
点评 本题考查了三角形中位线定理以及全等三角形的判定和性质,解题的关键是求AE:CE的值转化为求DM:CE的值.

练习册系列答案
相关题目
9.下列各组数据中,互为相反数的是( )
| A. | +(-3)和-(+3) | B. | -(-5)和+5 | C. | -(-6)和+(+6) | D. | +7和+(-7) |
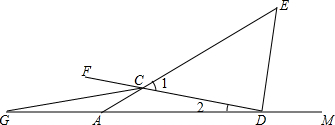 如图,∠CDM,∠FCA为△ACD的二个外角,射线DE、CG分别平分∠CDM、∠FCA,CG交DA的延长线交于点G.∠E=∠1,∠G=∠2,求∠ACD的度数.
如图,∠CDM,∠FCA为△ACD的二个外角,射线DE、CG分别平分∠CDM、∠FCA,CG交DA的延长线交于点G.∠E=∠1,∠G=∠2,求∠ACD的度数. 如图,△ABC中,∠C,∠B的平分线相交于O,过O作AO的垂线与边AB、AC分别交于D、E,求证:△BDO∽△BOC∽△OEC.
如图,△ABC中,∠C,∠B的平分线相交于O,过O作AO的垂线与边AB、AC分别交于D、E,求证:△BDO∽△BOC∽△OEC.