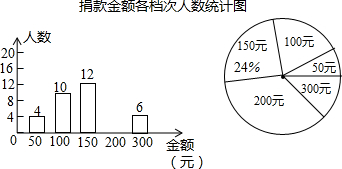
题目内容
6．已知实数x、y满足2x2+3x+y-1=0，则式子2x-y的最小值为-$\frac{33}{8}$．分析 把2x2+3x+y-1=0变形得到2x-y=2x2+5x-1，这样可以把2x-y看作是关于x的二次函数，然后利用配方法即可求出2x-y的最小值．
解答 解：∵2x2+3x+y-1=0，
∴y=-2x2-3x+1，
∴2x-y=2x+2x2+3x-1=2x2+5x-1，
∵2x2+5x-1=2（x2+$\frac{5}{2}$x）-1=2（x+$\frac{5}{4}$）2-$\frac{33}{8}$，
∴当x=$\frac{5}{4}$时，2x-y有最小值-$\frac{33}{8}$．
故答案为：-$\frac{33}{8}$．
点评 本题考查了配方法的应用，二次函数的最值问题，通过恒等变形得到2x-y是关于x的二次函数是解答此题的关键．
练习册系列答案
相关题目
17．下面结论正确的有（ ）
①两个有理数相加，和一定大于每一个加数．
②一个正数与一个负数相加得正数．
③倒数等于它本身的数仅有±1．
④两个正数相加，和为正数．
⑤两个负数相加，绝对值相减．
⑥正数加负数，其和一定等于0．
①两个有理数相加，和一定大于每一个加数．
②一个正数与一个负数相加得正数．
③倒数等于它本身的数仅有±1．
④两个正数相加，和为正数．
⑤两个负数相加，绝对值相减．
⑥正数加负数，其和一定等于0．
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
如图，在△ABC中，AB=10，AC=8．
1．在下列长度的四组线段中，能组成三角形的是（ ）
| A． | 3，7，15 | B． | 1，2，4 | C． | 5，5，10 | D． | 2，3，3 |
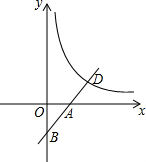如图，一次函数y=x+b（b为常数）的图象分别交坐标轴于A，B两点，y与反比例函数y=$\frac{\sqrt{2}}{x}$（x＞0）的图象交于点D，则AD•BD=2$\sqrt{2}$．
15．计算（-1）÷（-15）×15的结果是（ ）
| A． | -1 | B． | 1 | C． | $\frac{1}{225}$ | D． | -225 |
