题目内容
5.解下列方程组:(1)$\left\{\begin{array}{l}4x-3y=5\\ 4x+6y=14\end{array}\right.$
(2)$\left\{\begin{array}{l}3(x+y)-4(x-y)=4\\ \frac{x+y}{2}+\frac{x-y}{6}=1\end{array}\right.$.
分析 (1)②-①得出9y=9,求出y,把y的值代入①求出x即可;
(2)整理后①×2+②得出15y=11,求出y,①-②×7得出-15x=-17,求出x即可.
解答 解:(1)$\left\{\begin{array}{l}{4x-3y=5①}\\{4x+6y=14②}\end{array}\right.$
②-①得:9y=9,
解得:y=1,
把y=1代入①得:4x-3=5,
解得:x=2,
所以原方程组的解为:$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$;
(2)整理得:$\left\{\begin{array}{l}{-x+7y=4①}\\{2x+y=3②}\end{array}\right.$
①×2+②得:15y=11,
解得:y=$\frac{11}{15}$,
①-②×7得:-15x=-17,
解得:x=$\frac{17}{15}$,
所以原方程组的解为:$\left\{\begin{array}{l}{x=\frac{17}{15}}\\{y=\frac{11}{15}}\end{array}\right.$.
点评 本题考查了解二元一次方程组的应用,能把二元一次方程组转化成一元一次方程是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.马小虎的家距离学校1800米,一天马小虎从家去上学,出发10分钟后,爸爸发现他的数学课本忘记拿了,立即带上课本去追他,在距离学校200米的地方追上了他,已知爸爸的速度是马小虎速度的2倍,求马小虎的速度.设马小虎的速度为x米/分,则爸爸的速度是2x米/分,依据等量关系,列方程为( )
| A. | $\frac{1800-200}{x}=\frac{1800-200}{2x}+10$ | B. | $\frac{1800+200}{x}=\frac{1800+200}{2x}+10$ | ||
| C. | $\frac{1800-200}{x}=\frac{1800-200}{2x}-10$ | D. | $\frac{1800+200}{x}=\frac{1800+200}{2x}-10$ |
15.一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是( )


| A. | ($\frac{1}{2}$)2015 | B. | ($\frac{1}{2}$)2016 | C. | ($\frac{\sqrt{3}}{3}$)2016 | D. | ($\frac{\sqrt{3}}{3}$)2015 |
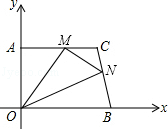 在平面直角坐标系中,直角梯形AOBC的位置图所示,∠OAC=90°,AC∥OB,OA=4,AC=5,OB=6.M、N分别在线段AC、线段BC上运动,当△MON的面积达到最大时,存在一种使得△MON周长最小的情况,则此时点M的坐标为(3,4).
在平面直角坐标系中,直角梯形AOBC的位置图所示,∠OAC=90°,AC∥OB,OA=4,AC=5,OB=6.M、N分别在线段AC、线段BC上运动,当△MON的面积达到最大时,存在一种使得△MON周长最小的情况,则此时点M的坐标为(3,4).