题目内容
如图，△ABC中，∠C=60°，AD，BE是高，AD、BE交于点O，求证：DE=| 1 |
| 2 |
考点：相似三角形的判定与性质,含30度角的直角三角形
专题：证明题
分析：先证明△CAD∽△CBE，可得
=
，即
=
，结合公共角可证明△CED∽△CBA，则可知
=
，结合∠C=60°可得结论．
| CE |
| CD |
| CB |
| CA |
| CE |
| CB |
| CD |
| CA |
| DE |
| AB |
| CE |
| CB |
解答：证明：∵AD、BE是高，
∴∠CEB=∠CDA，且∠ACD=∠BCE，
∴△CAD∽△CBE，
∴
=
，即
=
，且∠ECD=∠BCA，
∴△CED∽△CBA，
∴
=
，
∵∠C=60°，
∴BC=2CE，
∴
=
，
∴DE=
AB．
∴∠CEB=∠CDA，且∠ACD=∠BCE，
∴△CAD∽△CBE，
∴
| CE |
| CD |
| CB |
| CA |
| CE |
| CB |
| CD |
| CA |
∴△CED∽△CBA，
∴
| DE |
| AB |
| CE |
| CB |
∵∠C=60°，
∴BC=2CE，
∴
| DE |
| AB |
| 1 |
| 2 |
∴DE=
| 1 |
| 2 |
点评：本题主要考查相似三角形判定和性质，掌握相似三角形的对应边成比例是解题的关键，注意含特殊角的直角三角形的性质的应用．
练习册系列答案
相关题目
如图，在平面直角坐标系中，四边形ABCD各顶点坐标分别为A（0，3），B（2，4），C（4，3），D（2，1）．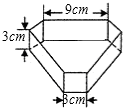
如图所示，是一种“口子窖”酒的包装纸盒，它的侧面由长方形和正方形组成．经测量，底面六变形有三条边的长是9cm，有三条边的长是3cm，每个内角都是120°，该六棱柱的高是3cm，请你设计一种裁剪方案，使之能制作这种无盖的包装盒．