题目内容
已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(2,0)、C(0,2)三点.
(1)求这条抛物线的解析式;
(2)如图一,点P是第一象限内此抛物线上的一个动点,当点P运动到什么位置时,四边形ABPC的面积最大?求出此时点P的坐标;
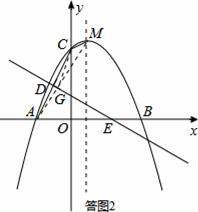
(3)如图二,设线段AC的垂直平分线交x轴于点E,垂足为D,M为抛物线的顶点,那么在直线DE上是否存在一点G,使△CMG的周长最小?若存在,请求出点G的坐标;若不存在,请说明理由.


【考点】二次函数综合题.
【专题】代数几何综合题.
【分析】方法一:
(1)利用待定系数法即可求得;
(2)如答图1,四边形ABPC由△ABC与△PBC组成,△ABC面积固定,则只需要使得△PBC面积最大即可.求出△PBC面积的表达式,然后利用二次函数性质求出最值;
(3)如答图2,DE为线段AC的垂直平分线,则点A、C关于直线DE对称.连接AM,与DE交于点G,此时△CMG的周长=CM+CG+MG=CM+AM最小,故点G为所求.分别求出直线DE、AM的解析式,联立后求出点G的坐标.
方法二:
(1)略.
(2)由于△ABC面积为定值,因此只需△BCP面积最大时,四边形ABPC的面积最大,利用水平底与铅垂高乘积的一半可求出P点坐标.
(3)因为点A,C关于直线DE对称,因此直线AM与直线DE的交点即为点G.联立AM与DE的直线方程,可求出G点坐标.
【解答】方法一:
解:(1)∵抛物线y=ax2+bx+c经过A(﹣1,0)、B(2,0)、C(0,2)三点.
∴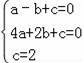
 ,解得
,解得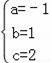
 ,
,
∴这条抛物线的解析式为:y=﹣x2+x+2.
(2)设直线BC的解析式为:y=kx+b,将B(2,0)、C(0,2)代入得:

 ,解得
,解得
 ,
,
∴直线BC的解析式为:y=﹣x+2.
如答图1,连接BC.
四边形ABPC由△ABC与△PBC组成,△ABC面积固定,则只需要使得△PBC面积最大即可.
设P(x,﹣x2+x+2),
过点P作PF∥y轴,交BC于点F,则F(x,﹣x+2).
∴PF=(﹣x2+x+2)﹣(﹣x+2)=﹣x2+2x.
S△PBC=S△PFC+S△PFB=
 PF(xF﹣xC)+
PF(xF﹣xC)+
 PF(xB﹣xF)=
PF(xB﹣xF)=
 PF(xB﹣xC)=PF
PF(xB﹣xC)=PF
∴S△PBC=﹣x2+2x=﹣(x﹣1)2+1
∴当x=1时,△PBC面积最大,即四边形ABPC面积最大.此时P(1,2).
∴当点P坐标为(1,2)时,四边形ABPC的面积最大.
(3)存在.
∵∠CAO+∠ACO=90°,∠CAO+∠AED=90°,
∴∠ACO=∠AED,又∵∠CAO=∠CAO,
∴△AOC∽△ADE,
∴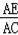
 =
=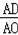
 ,即
,即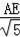
 =
=
 ,解得AE=
,解得AE=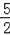
 ,
,
∴E(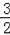
 ,0).
,0).
∵DE为线段AC的垂直平分线,
∴点D为AC的中点,∴D(﹣
 ,1).
,1).
可求得直线DE的解析式为:y=﹣
 x+
x+
 ①.
①.
∵y=﹣x2+x+2=﹣(x﹣
 )2+
)2+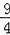
 ,∴M(
,∴M(
 ,
,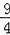
 ).
).
又A(﹣1,0),则可求得直线AM的解析式为:y=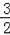
 x+
x+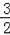
 ②.
②.
∵DE为线段AC的垂直平分线,
∴点A、C关于直线DE对称.
如答图2,连接AM,与DE交于点G,
此时△CMG的周长=CM+CG+MG=CM+AM最小,故点G为所求.
联立①②式,可求得交点G的坐标为(﹣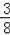
 ,
,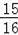
 ).
).
∴在直线DE上存在一点G,使△CMG的周长最小,点G的坐标为(﹣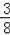
 ,
,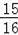
 ).
).
方法二:
(1)略.
(2)连接BC,过点P作x轴垂线,交BC′于F,
当△BCP面积最大时,四边形ABPC的面积最大.
∵B(2,0)、C(0,2),
∴lBC:y=﹣x+2,
设P(t,﹣t2+t+2),
∴F(t,﹣t+2),
S△BCP=
 (PY﹣FY)(BX﹣CX)=
(PY﹣FY)(BX﹣CX)=
 (﹣t2+t+2+t﹣2)×2=﹣t2+2t,
(﹣t2+t+2+t﹣2)×2=﹣t2+2t,
∴当t=1时,S△BCP有最大值,即四边形ABPC的面积最大.
∴P(1,2).
(3)∵DE为线段AC的垂直平分线,
∴点A是点C关于直线DE对称,
∴GC=GA,
∴△CMG的周长最小时,M,G,A三点共线.
∵抛物线y=﹣x2+x+2,
∴M(
 ,
,
 ),A(﹣1,0),
),A(﹣1,0),
∴lMA:y=
 x+
x+
 ,
,
∵A(﹣1,0),C(0,2),
∴KAC=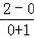
 =2,
=2,
∵AC⊥DE,∴KAC×KDE=﹣1,KDE=﹣
 ,
,
∵点D为AC的中点,
∴Dx=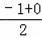
 =﹣
=﹣
 ,DY=
,DY=
 =1,
=1,
∴D(﹣
 ,1),
,1),
∴lDE:y=﹣
 x+
x+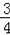
 ,
,
∴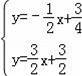
 ⇒
⇒
 ,
,
∴G(﹣
 ,
,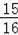
 ).
).


【点评】本题是二次函数综合题,难度适中,综合考查了二次函数的图象与性质、待定系数法求解析式、相似三角形、轴对称﹣最短路线、图形面积计算、最值等知识点.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案

 的顶点均在格点上,请在所给直角坐标系中按要求画图
的顶点均在格点上,请在所给直角坐标系中按要求画图
 成中心对称的
成中心对称的 ;
;
 都在双曲线
都在双曲线 上,
上, 分别是
分别是 轴,
轴, 轴上的动点,当四边形
轴上的动点,当四边形 的周长取最小值时,
的周长取最小值时, 所在直线的表达式为( )
所在直线的表达式为( ) A、
A、 B、
B、 C、
C、 D、
D、

 如图,函数
如图,函数 与
与 在同一平面直角坐标系中的图像大致( )
在同一平面直角坐标系中的图像大致( )



 ﹣
﹣



 若矩形纸片的一组对边与直角三角形的两条直角边相交成∠1、∠2,则∠2-∠
若矩形纸片的一组对边与直角三角形的两条直角边相交成∠1、∠2,则∠2-∠ 1=________
1=________