题目内容
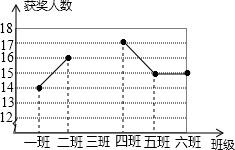 某中学组织网络安全知识竞赛活动,其中七年级6个班组每班参赛人数相同,学校对该年级的获奖人数进行统计,得到每班平均获奖15人,并制作成如图所示不完整的折线统计图.
某中学组织网络安全知识竞赛活动,其中七年级6个班组每班参赛人数相同,学校对该年级的获奖人数进行统计,得到每班平均获奖15人,并制作成如图所示不完整的折线统计图.(1)请将折线统计图补充完整,并直接写出该年级获奖人数最多的班级是
(2)若二班获奖人数占班级参赛人数的32%,则全年级参赛人数是
(3)若该年级并列第一名有男、女同学各2名,从中随机选取2名参加市级比赛,则恰好是1男1女的概率是
考点:折线统计图,列表法与树状图法
专题:图表型,数形结合
分析:(1)共有15×6=90人获奖,然后用90分别减去其他5个班的获奖人数即可得到三班获奖人数,然后将折线统计图补充完整,并且可得到四班有17人获奖,获奖人数最多;
(2)先计算出二班参赛人数,然后乘以6即可得到全年级参赛人数;
(3)先画树状图展示所有12种等可能的结果数,再找出恰好是1男1女所占的结果数,然后根据概率公式求解.
(2)先计算出二班参赛人数,然后乘以6即可得到全年级参赛人数;
(3)先画树状图展示所有12种等可能的结果数,再找出恰好是1男1女所占的结果数,然后根据概率公式求解.
解答:解 :(1)三班获奖人数=6×15-14-16-17-15-15=13,
:(1)三班获奖人数=6×15-14-16-17-15-15=13,
折线统计图如图,
该年级获奖人数最多的班级为四班;
(2)二班参赛人数=16÷32%=50(人),
所以全年级参赛人数=6×50=300(人);
(3)画树状图为: ,
,
共有12种等可能的结果数,其中恰好是1男1女占8种,
所以恰好是1男1女的概率=
=
.
 :(1)三班获奖人数=6×15-14-16-17-15-15=13,
:(1)三班获奖人数=6×15-14-16-17-15-15=13,折线统计图如图,
该年级获奖人数最多的班级为四班;
(2)二班参赛人数=16÷32%=50(人),
所以全年级参赛人数=6×50=300(人);
(3)画树状图为:
 ,
,共有12种等可能的结果数,其中恰好是1男1女占8种,
所以恰好是1男1女的概率=
| 8 |
| 12 |
| 2 |
| 3 |
点评:本题考查了折线统计图:折线图是用一个单位表示一定的数量,根据数量的多少描出各点,然后把各点用线段依次连接起来.以折线的上升或下降来表示统计数量增减变化.折线图不但可以表示出数量的多少,而且能够清楚地表示出数量的增减变化情况.也考查了列表法与树状图法.

练习册系列答案
相关题目
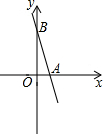 已知:如图,在平面直角坐标系xOy中,一次函数y=-4x+8的图象分别与x、y轴交于点A、B,点P在x轴的负半轴上,△ABP的面积为12.若一次函数y=kx+b的图象经过点P和点B,求这个一次函数y=kx+b表达式.
已知:如图,在平面直角坐标系xOy中,一次函数y=-4x+8的图象分别与x、y轴交于点A、B,点P在x轴的负半轴上,△ABP的面积为12.若一次函数y=kx+b的图象经过点P和点B,求这个一次函数y=kx+b表达式. 如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°
如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°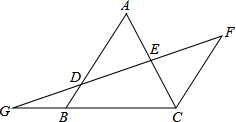 如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.
如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G. 某体育用品商店试销一款成本为50元的排球,规定试销期间单价不低于成本价,且获利不得高于40%.经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.
某体育用品商店试销一款成本为50元的排球,规定试销期间单价不低于成本价,且获利不得高于40%.经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.