题目内容
已知a,b,c为有理数,且a+b-c=0,abc<0,则
+
+
的值为( )
| b-c |
| |a| |
| a-c |
| |b| |
| a+b |
| |c| |
| A、-1 | B、1 | C、1或-1 | D、-3 |
考点:代数式求值,有理数的混合运算
专题:
分析:根据有理数的乘法判断出a、b、c三个数中有奇数个负数,再表示出b-c,a-c,a+b,然后分情况去掉绝对值号,求解即可.
解答:解:∵abc<0,
∴a、b、c三个数中有奇数个负数,
∵a+b-c=0,
∴b-c=-a,a-c=-b,a+b=c,
∴
+
+
=
+
+
,
若c是正数,则a、b有一个是负数,不妨设a是负数,
原式=
+
+
=1-1+1=1,
若c是负数,则a、b都是负数,
原式=
+
+
=1+1-1=1,
综上所述,代数式的值为1.
故选B.
∴a、b、c三个数中有奇数个负数,
∵a+b-c=0,
∴b-c=-a,a-c=-b,a+b=c,
∴
| b-c |
| |a| |
| a-c |
| |b| |
| a+b |
| |c| |
| -a |
| |a| |
| -b |
| |b| |
| c |
| |c| |
若c是正数,则a、b有一个是负数,不妨设a是负数,
原式=
| -a |
| -a |
| -b |
| b |
| c |
| c |
若c是负数,则a、b都是负数,
原式=
| -a |
| -a |
| -b |
| -b |
| c |
| -c |
综上所述,代数式的值为1.
故选B.
点评:本题考查了代数式求值,主要利用了有理数的乘法,绝对值的性质,难点在于从c的正负情况讨论.

练习册系列答案
相关题目
实数
-1的相反数是( )
| 2 |
A、-
| ||
B、
| ||
C、1-
| ||
D、-1+
|
 如图,在等腰Rt△ABC中,∠ACB=90°,点P是△ABC内一点,且CP=1,BP=
如图,在等腰Rt△ABC中,∠ACB=90°,点P是△ABC内一点,且CP=1,BP=| 2 |
| 2 |
| 2 |
| A、①②③ | B、①③④ |
| C、②③④ | D、①②④ |
将抛物线y=x2+1先向左平移2个单位,再向下平移3个单位,那么所得抛物线的函数关系式是( )
| A、y=(x+2)2+2 |
| B、y=(x+2)2-2 |
| C、y=(x-2)2+2 |
| D、y=(x-2)2-2 |
 如图,边长为a的正三角形的内切圆半径是( )
如图,边长为a的正三角形的内切圆半径是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
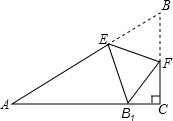 如图,在△ABC中,∠ACB=90°,∠A=30°,AB=6,点E、F分别在AB、BC上,沿EF将△EBF翻折,使顶点B的对应点B1落在AC上,若EB1⊥AC,则EF等于
如图,在△ABC中,∠ACB=90°,∠A=30°,AB=6,点E、F分别在AB、BC上,沿EF将△EBF翻折,使顶点B的对应点B1落在AC上,若EB1⊥AC,则EF等于