题目内容
7. 已知,如图,在△ABC中,CF平分∠ACB,CA=CD,AE=EB,求证:EF=$\frac{1}{2}$BD.
已知,如图,在△ABC中,CF平分∠ACB,CA=CD,AE=EB,求证:EF=$\frac{1}{2}$BD.
分析 由等腰三角形的性质可证明F为AD的中点,可得EF为△ABD的BD边上的中位线,可证得结论.
解答 证明:
∵CA=CD,CF平分∠ACB,
∴CF为AD边上的中线,
∴F为AD的中点,
又AE=EB,
∴E为AB中点,
∴EF为△ABD的BD边上的中位线,
∴EF=$\frac{1}{2}$BD.
点评 本题主要考查等腰三角形的性质和三角形中位线定理,利用等腰三角形“三线合一”的性质证得F为AD边的中点是解题的关键.

练习册系列答案
相关题目
15. 如图,在?ABCD中,点E、F分别在AB、CD上,且AE=CF,则四边形BFDE不可能是( )
如图,在?ABCD中,点E、F分别在AB、CD上,且AE=CF,则四边形BFDE不可能是( )
 如图,在?ABCD中,点E、F分别在AB、CD上,且AE=CF,则四边形BFDE不可能是( )
如图,在?ABCD中,点E、F分别在AB、CD上,且AE=CF,则四边形BFDE不可能是( )| A. | 矩形 | B. | 菱形 | C. | 梯形 | D. | 平行四边形 |
19.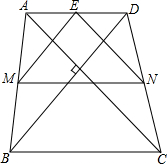 如图,在四边形ABCD中,AC=BD,且AC⊥BD,M,N分别是AB,CD的中点,E是AD的中点,则△EMN是( )
如图,在四边形ABCD中,AC=BD,且AC⊥BD,M,N分别是AB,CD的中点,E是AD的中点,则△EMN是( )
 如图,在四边形ABCD中,AC=BD,且AC⊥BD,M,N分别是AB,CD的中点,E是AD的中点,则△EMN是( )
如图,在四边形ABCD中,AC=BD,且AC⊥BD,M,N分别是AB,CD的中点,E是AD的中点,则△EMN是( )| A. | 等边三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 不能确定 |
16.已知x=3是方程x2-2x+a=0的根,则a等于( )
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
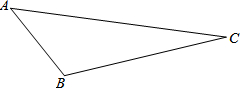 已知△ABC中,∠ABC为钝角.请你按要求作图(不写作法,但要
已知△ABC中,∠ABC为钝角.请你按要求作图(不写作法,但要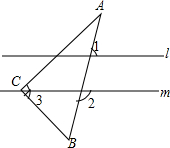 如图,一块含30°角的直角三角板ABC (∠C=90°,∠A=30°)的直角顶点C放置在直线m上,且l∥m,∠1=70°,则∠2=110°,∠3=50°.
如图,一块含30°角的直角三角板ABC (∠C=90°,∠A=30°)的直角顶点C放置在直线m上,且l∥m,∠1=70°,则∠2=110°,∠3=50°.