题目内容
 如图,B、D、F在AN上,C、E在AM上,且AB=BC=CD,EC=ED=EF,∠A=20°,求∠FEM的度数.
如图,B、D、F在AN上,C、E在AM上,且AB=BC=CD,EC=ED=EF,∠A=20°,求∠FEM的度数.考点:等腰三角形的性质
专题:
分析:根据三角形内角和定理,三角形外角和内角的关系以及等腰三角形的性质,逐步推出∠FEM的度数.
解答:解:∵∠A=20°,AB=BC,
∴∠A=∠ACB=20°,∠CBD=∠A+∠ACB=20°+20°=40°;
∵BC=CD,
∴∠CBD=∠CDB=40°,
∴∠ECD=∠A+∠CDA=30°(外角定理);
∵CD=DE,
∴∠DCE=∠DEC=50°,
∴∠EDF=∠A+∠AED=60°;
又∵DE=EF,
∴∠EDF=∠EFD=60°,
∴∠FEM∠A+∠EFD=20°+60°=80°.
∴∠A=∠ACB=20°,∠CBD=∠A+∠ACB=20°+20°=40°;
∵BC=CD,
∴∠CBD=∠CDB=40°,
∴∠ECD=∠A+∠CDA=30°(外角定理);
∵CD=DE,
∴∠DCE=∠DEC=50°,
∴∠EDF=∠A+∠AED=60°;
又∵DE=EF,
∴∠EDF=∠EFD=60°,
∴∠FEM∠A+∠EFD=20°+60°=80°.
点评:本题综合考查了等腰三角形的性质、三角形内角和定理、三角形外角性质.此类题考生应该注意的是三角形内角和定理、外角性质的运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,CA=CB,则数轴上点A所表示的数是( )
如图,CA=CB,则数轴上点A所表示的数是( )A、
| ||
B、
| ||
C、2-
| ||
D、3-
|

 如图,在?ABCD中,AE⊥BC于E点,点E为BC的中点,tanB=2,点P在BE上,作EF⊥DP于点F,连结AF.
如图,在?ABCD中,AE⊥BC于E点,点E为BC的中点,tanB=2,点P在BE上,作EF⊥DP于点F,连结AF. 如图△ABC中,BA⊥AC,CF⊥FB,D是BC的中点,DE⊥AF,∠CBF=30°.
如图△ABC中,BA⊥AC,CF⊥FB,D是BC的中点,DE⊥AF,∠CBF=30°.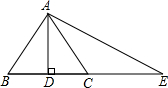 如图,AB=AC,AD⊥BC,点C在线段AE的垂直平分线上,在不添加任何线或字母情况下,问AB+BD会与图中哪条线段相等?答:是
如图,AB=AC,AD⊥BC,点C在线段AE的垂直平分线上,在不添加任何线或字母情况下,问AB+BD会与图中哪条线段相等?答:是