题目内容
13.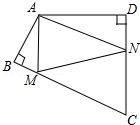 如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )| A. | 110° | B. | 120° | C. | 130° | D. | 140° |
分析 作点A关于BC的对称点A′,关于CD的对称点A″,根据轴对称确定最短路线问题,连接A′A″与BC、CD的交点即为所求的点M、N,利用三角形的内角和定理列式求出∠A′+∠A″,再根据轴对称的性质和三角形的一个外角等于与它不相邻的两个内角的和可得∠AMN+∠ANM=2(∠A′+∠A″),然后计算即可得解.
解答 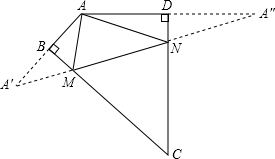 解:如图,作点A关于BC的对称点A′,关于CD的对称点A″,
解:如图,作点A关于BC的对称点A′,关于CD的对称点A″,
连接A′A″与BC、CD的交点即为所求的点M、N,
∵∠BAD=110°,∠B=∠D=90°,
∴∠A′+∠A″=180°-110°=70°,
由轴对称的性质得:∠A′=∠A′AM,∠A″=∠A″AN,
∴∠AMN+∠ANM=2(∠A′+∠A″)=2×70°=140°.
故选:D.
点评 本题考查了轴对称确定最短路线问题,轴对称的性质,三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,确定出点M、N的位置是解题的关键,要注意整体思想的利用.

练习册系列答案
相关题目
4.如果a是有理数,则下列各数中一定是正数的是( )
| A. | 2016a | B. | 2016+a | C. | |a| | D. | a2+0.0001 |
1.下列根式中,不是二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{4}$ | C. | $\sqrt{{a}^{2}}$ | D. | $\sqrt{-3}$ |
8.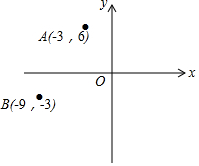 如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为3:1,把△ABO放大,则点A的对应点A′的坐标是( )
如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为3:1,把△ABO放大,则点A的对应点A′的坐标是( )
 如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为3:1,把△ABO放大,则点A的对应点A′的坐标是( )
如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为3:1,把△ABO放大,则点A的对应点A′的坐标是( )| A. | (-1,2) | B. | (-9,18) | C. | (-9,18)或(9,-18) | D. | (-1,2)或(1,-2) |
18.A、B两个动点在数轴上做匀速运动,它们的运动时间以及位置记录如表.
(1)根据题意,填写下列表格;
(2)A、B两点能否相遇,如果相遇,求相遇时的时刻及在数轴上的位置;如果不能相遇,请说明理由;
(3)A、B两点能否相距9个单位长度?如果能,求相距9个单位长度的时刻;如不能,请说明理由.
(1)根据题意,填写下列表格;
| 时间(秒) | 0 | 5 | 7 |
| A点位置 | 19 | -1 | -9 |
| B点位置 | -8 | 17 | 27 |
(3)A、B两点能否相距9个单位长度?如果能,求相距9个单位长度的时刻;如不能,请说明理由.
5.已知点O是线段AB上的一点,且AB=12cm,点M、N分别是线段AO、线段BO的中点,那么线段MN的长度是( )
| A. | 6cm | B. | 5cm | C. | 4cm | D. | 无法确定 |