题目内容
5．已知点O是线段AB上的一点，且AB=12cm，点M、N分别是线段AO、线段BO的中点，那么线段MN的长度是（ ）| A． | 6cm | B． | 5cm | C． | 4cm | D． | 无法确定 |
分析 根据线段中点的性质，可得OM，ON，根据线段的和差，可得答案．
解答 解：由题意，得
AO+BO=12．
点M、N分别是线段AO、线段BO的中点，得
MO=$\frac{1}{2}$AO，NO=$\frac{1}{2}$BO．
MN=MO+NO=$\frac{1}{2}$（AO+BO）=6cm，
故选：A．
点评 本题考查了两点间的距离，利用线段中点的性质得出MO=$\frac{1}{2}$AO，NO=$\frac{1}{2}$BO是解题关键．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
13．
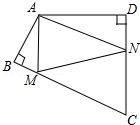如图，四边形ABCD中，∠BAD=110°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使△AMN周长最小时，则∠AMN+∠ANM的度数为（ ）
如图，四边形ABCD中，∠BAD=110°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使△AMN周长最小时，则∠AMN+∠ANM的度数为（ ）| A． | 110° | B． | 120° | C． | 130° | D． | 140° |
20．已知圆柱的底面半径为3cm，母线长为6cm，则圆柱的侧面积是（ ）
| A． | 36cm2 | B． | 36π cm2 | C． | 18cm2 | D． | 18π cm2 |
17．探究题．
用棋子摆成的“T”字形图如图所示：
（1）填写表：
（2）写出第n个“T”字形图案中棋子的个数（用含n的代数式表示）；
（3）第20个“T”字形图案共有棋子多少个？
（4）计算前20个“T”字形图案中棋子的总个数．（提示：请你先思考下列问题：第1个图案与第20个图案中共有多少个棋子？第2个图案与第19个图案中共有多少个棋子？第3个图案与第18个图案呢？）
用棋子摆成的“T”字形图如图所示：
（1）填写表：
| 图形序号 | ① | ② | ③ | ④ | … | ⑩ |
| 每个图案中棋子个数 | 5 | 8 | … |
（3）第20个“T”字形图案共有棋子多少个？
（4）计算前20个“T”字形图案中棋子的总个数．（提示：请你先思考下列问题：第1个图案与第20个图案中共有多少个棋子？第2个图案与第19个图案中共有多少个棋子？第3个图案与第18个图案呢？）
a、b在数轴上的位置如图所示，化简|a-b|-$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{（b-a）^{2}}$．