题目内容
7. 如图:在△ABC中,点D在AB边上,点E在AC边的延长线上,CE=BD,DG=GE.求证:AB=AC.
如图:在△ABC中,点D在AB边上,点E在AC边的延长线上,CE=BD,DG=GE.求证:AB=AC.
分析 利用平行线的性质得出∠FDG=∠CEG,∠DFG=∠ECG,因此∠DFB=∠ACB,利用ASA得出△GDF≌△GEC,再利用全等三角形的性质以及等腰三角形的判定得出即可.
解答 证明:过点D作DF∥AE交BC于F,如图所示:
则∠FDG=∠CEG,∠DFG=∠ECG,
∴∠DFB=∠ACB,
在△GDF和△GEC中,$\left\{\begin{array}{l}{∠FDG=∠CEG}&{\;}\\{DG=GE}&{\;}\\{∠DGF=∠EGC}&{\;}\end{array}\right.$,
∴△GDF≌△GEC(ASA),
∴DF=CE,
又∵BD=CE,
∴BD=DF,
∴∠DBF=∠DFB,
∴∠DBF=∠ACB,
即∠ABC=∠ACB,
∴AB=AC.
点评 本题考查了全等三角形的判定与性质、等腰三角形的判定、平行线的性质;熟练掌握等腰三角形的判定,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
2.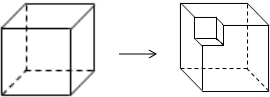 如图,从一个棱长为3cm的正方体的一顶点处挖去一个棱长为1cm的正方体,则剩余部分的体积和表面积分别是( )
如图,从一个棱长为3cm的正方体的一顶点处挖去一个棱长为1cm的正方体,则剩余部分的体积和表面积分别是( )
 如图,从一个棱长为3cm的正方体的一顶点处挖去一个棱长为1cm的正方体,则剩余部分的体积和表面积分别是( )
如图,从一个棱长为3cm的正方体的一顶点处挖去一个棱长为1cm的正方体,则剩余部分的体积和表面积分别是( )| A. | 27cm3,54cm2 | B. | 26cm3,54cm2 | C. | 27cm3,51cm2 | D. | 26cm3,51cm2 |
 (1)如图,点D在△ABC中,写出图中所有三角形:△ABD,△ADC,△BDC,△ABC
(1)如图,点D在△ABC中,写出图中所有三角形:△ABD,△ADC,△BDC,△ABC 如图,四边形ABCD中,∠DAB=∠ABC=90°,AB=BC,E是AB的中点,CE⊥BD.
如图,四边形ABCD中,∠DAB=∠ABC=90°,AB=BC,E是AB的中点,CE⊥BD.