题目内容
19.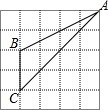 如图,在5×5的正方形网格中,△ABC的三个顶点A,B,C均在格点上,则tanA的值为$\frac{1}{3}$.
如图,在5×5的正方形网格中,△ABC的三个顶点A,B,C均在格点上,则tanA的值为$\frac{1}{3}$.
分析 根据勾股定理,可得BD、AD的长,根据正切为对边比邻边,可得答案.
解答 解:如图:作BD⊥AC于D ,
,
BD=$\sqrt{2}$,AD=3$\sqrt{2}$,
tanA=$\frac{BD}{AD}$=$\frac{\sqrt{2}}{3\sqrt{2}}$=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$.
点评 本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
相关题目
8.下列关系式中,属于二次函数的是(x为自变量)( )
| A. | y=ax2+bx+c | B. | $y=\sqrt{{x^2}-1}$ | C. | $y=\frac{1}{x^2}$ | D. | $y=\frac{1}{8}{x^2}$ |
9.一台电冰箱的原价是2400元,现在按七折出售,求现价多少元?列式是( )
| A. | 2400÷70% | B. | 2400×70% | C. | 2400×(1-70%) | D. | 2400×7 |
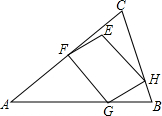 如图,在△ABC中,AB=AC=1,∠A=36°,?EFGH的顶点F,G,H分别在AC,AB,BC边上,且FC=CH.
如图,在△ABC中,AB=AC=1,∠A=36°,?EFGH的顶点F,G,H分别在AC,AB,BC边上,且FC=CH.