题目内容
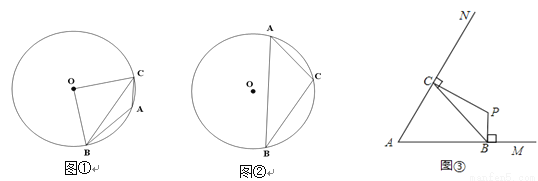
已知A、B、C三点不在同一直线上.
(1)若点A、B、C均在半径为R的⊙O上,
①如图①,当∠A=135°,R=1时,求∠BOC的度数和BC的长.
②如图②,当∠A为锐角时,求证: 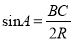 ;
;
(2)若定长线段BC的两个端点分别在∠MAN的两边AM、AN(B、C均与A不重合)滑动,如图③,当∠MAN=60°,BC=2时,分别作BP⊥AM,CP⊥AN,交点为P,试探索在整个滑动过程中,P、A两点间的距离是否保持不变?请说明理由.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 B.
B.  C.
C.  D.
D.