题目内容
 如图,AB是⊙O的切线,切点为A,OA=1,∠AOB=60°,则图中阴影部分的面积是
如图,AB是⊙O的切线,切点为A,OA=1,∠AOB=60°,则图中阴影部分的面积是考点:切线的性质,扇形面积的计算
专题:
分析:在RT△OAB中,得出AB的长度,求出△OAB的面积,然后求出扇形OAC的面积,再由阴影部分的面积=三角形OAB的面积-扇形OAC的面积即可得出答案.
解答:解:∵AB是⊙O的切线,切点为A,
∴OA⊥AB,即∠OAB=90°.
∵在Rt△AOB中,OA=1,∠AOB=60°,
∴AB=OAtan∠AOB=
.
∴S阴影部分=S△AOB-S扇形OAC=
•1•
-
=
-
π.
故答案为:
-
π.
∴OA⊥AB,即∠OAB=90°.
∵在Rt△AOB中,OA=1,∠AOB=60°,
∴AB=OAtan∠AOB=
| 3 |
∴S阴影部分=S△AOB-S扇形OAC=
| 1 |
| 2 |
| 3 |
| 60•π•12 |
| 360 |
| ||
| 2 |
| 1 |
| 6 |
故答案为:
| ||
| 2 |
| 1 |
| 6 |
点评:此题考查了扇形面积计算及切线的性质,属于基础题,解答本题的关键是判断出△OAB是直角三角形,难度一般.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
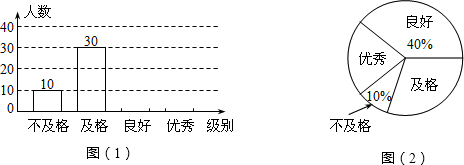
 某海防哨所O发现在他的东偏北60°方向,距离哨所400m的A处有一艘船向正东方向航行,经过2分钟后到达哨所的东北方向的B处,问船从A处到B处航速是多少千米/小时(精确到1千米/小时)?(参考数据
某海防哨所O发现在他的东偏北60°方向,距离哨所400m的A处有一艘船向正东方向航行,经过2分钟后到达哨所的东北方向的B处,问船从A处到B处航速是多少千米/小时(精确到1千米/小时)?(参考数据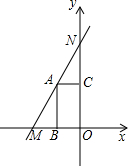 如图,点N(0,6),点M在x轴负半轴上,ON=3OM.A为线段MN上一点,AB⊥x轴,垂足为B,AC⊥y轴,垂足为C.矩形ABOC的面积为2.
如图,点N(0,6),点M在x轴负半轴上,ON=3OM.A为线段MN上一点,AB⊥x轴,垂足为B,AC⊥y轴,垂足为C.矩形ABOC的面积为2.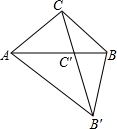 如图,在三角形ABC中,∠A=40°,△ABC绕点A旋转后点C落在边AB上的点C′,点B落到点B′,如果点C、C′、B′在同一直线上,那么∠ABC的度数是
如图,在三角形ABC中,∠A=40°,△ABC绕点A旋转后点C落在边AB上的点C′,点B落到点B′,如果点C、C′、B′在同一直线上,那么∠ABC的度数是