题目内容
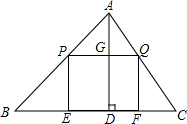 如图,在△ABC中,AD是BC边上的高,点G在AD上,过G作BC的平行线分别与AB、AC交于P、Q两点,过点P作PE⊥BC于点E,过点Q作QF⊥BC于点F.设AD=80,BC=120,当四边形PEFQ为正方形时,试求此正方形的边长.
如图,在△ABC中,AD是BC边上的高,点G在AD上,过G作BC的平行线分别与AB、AC交于P、Q两点,过点P作PE⊥BC于点E,过点Q作QF⊥BC于点F.设AD=80,BC=120,当四边形PEFQ为正方形时,试求此正方形的边长.考点:相似三角形的判定与性质,正方形的性质
专题:
分析:证明GD=PE=PQ;证明△APQ∽△ABC,列出比例式即可解决问题.
解答: 解:∵四边形PEFQ为正方形,且AD⊥BC,
解:∵四边形PEFQ为正方形,且AD⊥BC,
∴GD=PE=PQ(设为λ),
∴AG=80-λ;
∵PQ∥BC,
∴△APQ∽△ABC,
∴
=
,即
=
,
解得:λ=48,
即此时正方形的边长为48.
 解:∵四边形PEFQ为正方形,且AD⊥BC,
解:∵四边形PEFQ为正方形,且AD⊥BC,∴GD=PE=PQ(设为λ),
∴AG=80-λ;
∵PQ∥BC,
∴△APQ∽△ABC,
∴
| AG |
| AD |
| PQ |
| BC |
| 80-λ |
| 80 |
| λ |
| 120 |
解得:λ=48,
即此时正方形的边长为48.
点评:该题主要考查了相似三角形的判定及其性质的应用;应牢固掌握相似三角形的判定及其性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
据统计,2014年我国用义务教育经费支持了13940000名农民工随迁子女在城市里接受义务教育,这个数字精确到百万位后用科学记数法可表示为( )
| A、1.39×107 |
| B、1.4×107 |
| C、1.40×107 |
| D、13.94×107 |
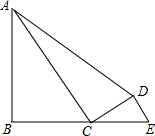 如图,在四边形ABCD中,∠B=∠ACD,过D作AC∥DE交BC的延长线于点E,且CD2=AC•DE
如图,在四边形ABCD中,∠B=∠ACD,过D作AC∥DE交BC的延长线于点E,且CD2=AC•DE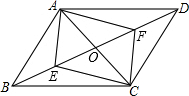 如图,在平行四边形ABCD中AC,BD相交于点O,E,F分别是OB、OD的中点.
如图,在平行四边形ABCD中AC,BD相交于点O,E,F分别是OB、OD的中点.