题目内容
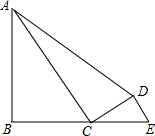 如图,在四边形ABCD中,∠B=∠ACD,过D作AC∥DE交BC的延长线于点E,且CD2=AC•DE
如图,在四边形ABCD中,∠B=∠ACD,过D作AC∥DE交BC的延长线于点E,且CD2=AC•DE(1)求证:∠DAC=∠DCE;
(2)若AD2=AB•AD+AC•DE,求证:∠ACD=90°.
考点:相似三角形的判定与性质
专题:证明题
分析:(1)证明∠ACD=∠CDE,
=
,得到△ACD∽△CDE,即可解决问题.
(2)证明∠ACB=∠ADC,此为解题的关键性结论;结合∠B=∠ACD,得到△ABC∽△ACD,进而证明AC2=AD•AB,结合已知条件证明AD2=AC2+CD2,即可解决问题.
| CD |
| AC |
| DE |
| CD |
(2)证明∠ACB=∠ADC,此为解题的关键性结论;结合∠B=∠ACD,得到△ABC∽△ACD,进而证明AC2=AD•AB,结合已知条件证明AD2=AC2+CD2,即可解决问题.
解答: 证明:(1)如图,∵AC∥DE,
证明:(1)如图,∵AC∥DE,
∴∠ACD=∠CDE;
又∵CD2=AC•DE,
∴
=
;
∴△ACD∽△CDE,
∴∠DAC=∠DCE.
(2)∵△ACD∽△CDE,
∴∠ADC=∠E;
∵AC∥DE,
∴∠ACB=∠E,
∴∠ACB=∠ADC;
∵∠B=∠ACD,
∴△ABC∽△ACD,
∴
=
,
∴AC2=AD•AB,
∵AD2=AB•AD+AC•DE,CD2=AC•DE,
∴AD2=AC2+CD2,
∴∠ACD=90°.
 证明:(1)如图,∵AC∥DE,
证明:(1)如图,∵AC∥DE,∴∠ACD=∠CDE;
又∵CD2=AC•DE,
∴
| CD |
| AC |
| DE |
| CD |
∴△ACD∽△CDE,
∴∠DAC=∠DCE.
(2)∵△ACD∽△CDE,
∴∠ADC=∠E;
∵AC∥DE,
∴∠ACB=∠E,
∴∠ACB=∠ADC;
∵∠B=∠ACD,
∴△ABC∽△ACD,
∴
| AC |
| AD |
| AB |
| AC |
∴AC2=AD•AB,
∵AD2=AB•AD+AC•DE,CD2=AC•DE,
∴AD2=AC2+CD2,
∴∠ACD=90°.
点评:该题主要考查了相似三角形的判定及其性质的应用问题;牢固掌握判定定理及性质定理是灵活解题的基础和关键.

练习册系列答案
相关题目
有某种三色冰淇淋50克,咖啡色、红色和白色配料的比是2:3:5,这种三色冰淇淋中咖啡色是多少克?( )
| A、10 | B、15 | C、20 | D、25 |
1纳米=0.000000001米,则15纳米用科学记数法可以表示为( )
| A、15×10-9 |
| B、1.5×10-10 |
| C、1.5×10-8 |
| D、1.5×10-9 |

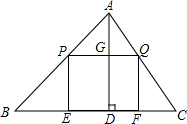 如图,在△ABC中,AD是BC边上的高,点G在AD上,过G作BC的平行线分别与AB、AC交于P、Q两点,过点P作PE⊥BC于点E,过点Q作QF⊥BC于点F.设AD=80,BC=120,当四边形PEFQ为正方形时,试求此正方形的边长.
如图,在△ABC中,AD是BC边上的高,点G在AD上,过G作BC的平行线分别与AB、AC交于P、Q两点,过点P作PE⊥BC于点E,过点Q作QF⊥BC于点F.设AD=80,BC=120,当四边形PEFQ为正方形时,试求此正方形的边长.