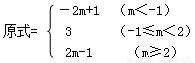题目内容
如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,-2).
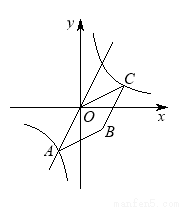
(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移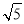 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
(1)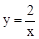 ;(2)为﹣1<x<0或x>1 ;(3)四边形OABC是菱形.
;(2)为﹣1<x<0或x>1 ;(3)四边形OABC是菱形.
【解析】
试题分析:(1)设反比例函数的解析式为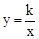 (k>0),先利用y=2x求出点A的坐标,然后代入即可;
(k>0),先利用y=2x求出点A的坐标,然后代入即可;
(2)根据函数图像解答即可;(3)观察图形猜想:四边形OABC是菱形,先证明四边形OABC是平行四边形,然后再证明OC=OA即可.
试题解析:
【解析】
(1)设反比例函数的解析式为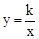 (k>0)
(k>0)
∵A(m,﹣2)在y=2x上
∴﹣2=2m
∴m=﹣1
∴A(﹣1,﹣2)
又∵点A在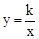 上
上
∴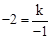
∴k=2,∴反比例函数的解析式为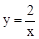 3分
3分
(2)由图知:正比例函数值大于反比例函数值时自变量x的取值范围为﹣1<x<0或x>1 5分
(3)四边形OABC是菱形.证明如下:
∵A(﹣1,﹣2)∴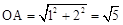
由题意知:CB∥OA且CB=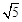 ,∴CB=OA
,∴CB=OA
∴四边形OABC是平行四边形 7分
∵C(2,n)在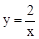 上,∴
上,∴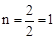 ,∴C(2,1),∴
,∴C(2,1),∴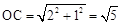 ,∴OC=OA
,∴OC=OA
∴平行四边形OABC是菱形。 10分
考点:1.反比例函数;2.函数图像与不等式;3.菱形的判定.

练习册系列答案
相关题目
 = .
= . 
 D.m+n≤
D.m+n≤ B.-
B.- =2
=2 =±2 D.
=±2 D. ×
× =
=
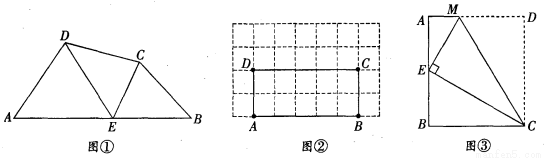
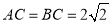 ,反比例
,反比例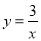 (
(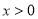 )的图象分别与AB,BC交于点D,E.连接DE,当△BDE∽△BCA时,点E的坐标为______________.
)的图象分别与AB,BC交于点D,E.连接DE,当△BDE∽△BCA时,点E的坐标为______________.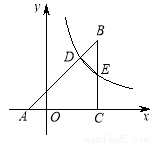
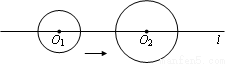

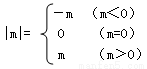 ,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|m+1|+|m-2|时,可令m+1=0和m-2=0,分别求得m=-1,m=2(称-1,2分别为|m+1|与|m-2|的零点值).在实数范围内,零点值m=-1和m=2可将全体实数分成不重复且不遗漏的如下3种情况:
,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|m+1|+|m-2|时,可令m+1=0和m-2=0,分别求得m=-1,m=2(称-1,2分别为|m+1|与|m-2|的零点值).在实数范围内,零点值m=-1和m=2可将全体实数分成不重复且不遗漏的如下3种情况: