题目内容
(13分)阅读下列材料并解决有关问题:
我们知道, 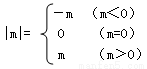 ,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|m+1|+|m-2|时,可令m+1=0和m-2=0,分别求得m=-1,m=2(称-1,2分别为|m+1|与|m-2|的零点值).在实数范围内,零点值m=-1和m=2可将全体实数分成不重复且不遗漏的如下3种情况:
,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|m+1|+|m-2|时,可令m+1=0和m-2=0,分别求得m=-1,m=2(称-1,2分别为|m+1|与|m-2|的零点值).在实数范围内,零点值m=-1和m=2可将全体实数分成不重复且不遗漏的如下3种情况:
(1)m<-1;(2)-1≤m<2;(3)m≥2.从而化简代数式|m+1|+|m-2|可分以下3种情况:
(1)当m<-1时,原式=-(m+1)-(m-2)=-2m+1;
(2)当-1≤m<2时,原式=m+1-(m-2)=3;
(3)当m≥2时,原式=m+1+m-2=2m-1.
综上讨论,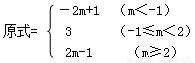
通过以上阅读,请你解决以下问题:
(1)分别求出|x-5|和|x-4|的零点值;
(2)化简代数式|x-5|+|x-4|.
(3) 求代数式|x-5|+|x-4|的最小值.
(1)x=5和x=4 (2) (3)1
(3)1
【解析】
试题分析:(1)零点值就是指当绝对值为零的时候x的值;(2)根据零点值将x的值分成三块进行讨论,然后分别计算;(3)根据化简的结果找出最小值.
试题解析:(1)当x-5=0时,即x=5;当x-4=0时,即x=4.∴|x-5|的零点值为x=5;|x-4|的零点值为x=4.
(2)当x<4时,原式=5-x+4-x=9-2x;
当4≤x<5时,原式=5-x+x-4=1;
当x≥5时,原式=x-5+x-4=2x-9;
综上所述,
(3)根据(2)得:代数式|x-5|+|x-4|的最小值为1.
考点:绝对值的化简

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
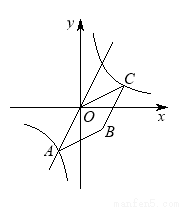
 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.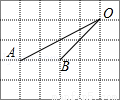
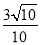 B.
B.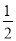 C.
C.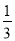 D.
D.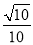
 中,自变量x的取值范围是______________。
中,自变量x的取值范围是______________。 与火车在隧道内的长度
与火车在隧道内的长度 之间的关系用图象描述大致是( )
之间的关系用图象描述大致是( )


 ※
※ =
= ,则3※(-3)的值等于 .
,则3※(-3)的值等于 . x的图象相交于点(2,m).
x的图象相交于点(2,m). 的两根分别为
的两根分别为 、
、 ,则
,则 的值为( )
的值为( ) C.4 D.
C.4 D.