题目内容
(本题满分10分) 如图①,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形AB-CD的边AB上的“强相似点”,解决问题:
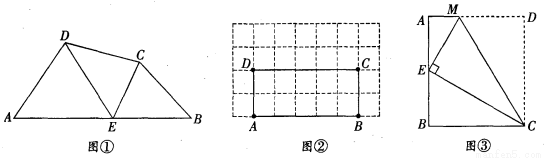
(1)如图①,∠A=∠B=∠DEC=45°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由:
(2)如图②,在矩形ABCD中,A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;
(3)如图③,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系.
见解析
【解析】
试题分析:(1)只要证明△ADE∽△BEC,即可证明点E是四边形ABCD的AB边上的相似点;(2)以CD为直径画弧,取该弧与AB的一个交点即为所求;(3)根据题意可得△AEM∽△BCE∽△ECM,然后利用相似三角形的对应角相等,可求得∠BCE= 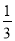 ∠BCD=30°,利用特殊角的三角函数值可得BE与AB,BC边之间的数量关系,从而可求出AB与BC边之间的数量关系.
∠BCD=30°,利用特殊角的三角函数值可得BE与AB,BC边之间的数量关系,从而可求出AB与BC边之间的数量关系.
试题解析:【解析】
(1)∵∠A=∠B=∠DEC=45°,∴∠AED+∠ADE=135°,∠AED+∠CEB=135°,∴∠ADE=∠CEB,
在△ADE和△BEC中,∠A=∠B,∠ADE=∠BEC,,∴△ADE∽△BEC,
∴点E是四边形ABCD的边AB上的相似点.
(2)如图所示:点E是四边形ABCD的边AB上的强相似点,

(3)∵点E是四边形ABCM的边AB上的一个强相似点,∴△AEM∽△BCE∽△ECM,∴∠BCE=∠ECM=∠AEM.
由折叠可知:△ECM≌△DCM,∴∠ECM=∠DCM,CE=CD,∴∠BCE=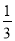 ∠BCD=30°,BE=
∠BCD=30°,BE=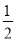 CE=
CE= AB,
AB,
在Rt△BCE中,tan∠BCE=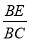 =tan30°=
=tan30°=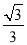 ,∴
,∴ .
.
考点:1.相似三角形的判定与性质;2. 图形折叠的性质;3. 特殊角的三角函数值.

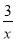 ,②
,②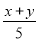 ,③
,③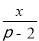 ,④
,④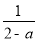 中,是分式的有
中,是分式的有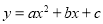 的对称轴为
的对称轴为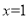 ,与
,与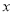 轴的一个交点
轴的一个交点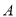 在(2,0)和(3,0)之间,其
在(2,0)和(3,0)之间,其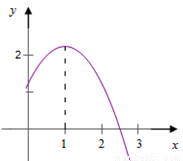
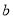 <
<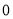 B.
B.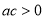 C.
C.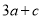
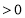 D.
D.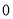
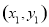 ,
,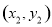 在函数
在函数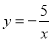 的图象上,当
的图象上,当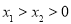 时,下列结论正确的是( ).
时,下列结论正确的是( ).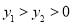 B.
B.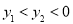 C.
C.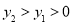 D.
D.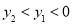

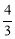 ,则t的值为
,则t的值为 
 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
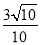 B.
B.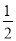 C.
C.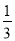 D.
D.