题目内容
7. 如图,在Rt△ABC中,∠ABC=90°∠A=30°,AC=10,把Rt△ABC绕点B顺时针旋转到△A′BC′的位置,点C′在AC上,A′C′与AB相交于点D,则C′D的长为$\frac{5}{2}$.
如图,在Rt△ABC中,∠ABC=90°∠A=30°,AC=10,把Rt△ABC绕点B顺时针旋转到△A′BC′的位置,点C′在AC上,A′C′与AB相交于点D,则C′D的长为$\frac{5}{2}$.
分析 根据在Rt△ABC中,∠ABC=90°∠A=30°,AC=10,可以求得BC的长,∠C的度数,又因为Rt△ABC绕点B顺时针旋转到△A′BC′的位置,点C′在AC上,A′C′与AB相交于点D,可以求得旋转前后的对应边和对应角是相等的,从而可以得到C′D的长,本题得以解决.
解答 解:∵在Rt△ABC中,∠ABC=90°∠A=30°,AC=10,
∴$BC=\frac{1}{2}AC=5$,∠C=60°,
∵Rt△ABC绕点B顺时针旋转到△A′BC′的位置,点C′在AC上,A′C′与AB相交于点D,∠C=60°,
∴BC=BC′,∠BC′D=∠C=60°,
∴△CBC′是等边三角形,
∴CC′=BC=5,∠CC′B=60°,
∴∠AC′D=60°,
∵∠A=30°,AC=10,CC′=5,
∴∠ADC′=90°,AC′=5,
∴C′D=$\frac{1}{2}AC′=\frac{5}{2}$.
故答案为:$\frac{5}{2}$.
点评 本题考查旋转的性质,解题的关键是明确在直角三角形中30°角所对的直角边等于斜边的一半和明确旋转前后对应边和对应角是相等的.

练习册系列答案
相关题目
12.方程x2+2x=0的解是( )
| A. | x1=0,x2=2 | B. | x1=0,x2=-2 | C. | x=2 | D. | x=-2 |
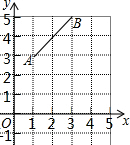 如图,在平面直角坐标系中,把线段AB先向右平移2个单位,再向下平移3个单位,得到线段CD,请画出线段CD并分别写出点A、B、C、D的坐标.
如图,在平面直角坐标系中,把线段AB先向右平移2个单位,再向下平移3个单位,得到线段CD,请画出线段CD并分别写出点A、B、C、D的坐标. 画出△ABC关于直线l的对称图形.
画出△ABC关于直线l的对称图形. 如图是某个正方体的表面展开图,各个面上分别标有1-6的不同数字,若将其折叠成正方体,则相交于同一个顶点的三个面上的数字之和最大的是13.
如图是某个正方体的表面展开图,各个面上分别标有1-6的不同数字,若将其折叠成正方体,则相交于同一个顶点的三个面上的数字之和最大的是13.