题目内容
14.已知两直线y1=2x-3,y2=6-x.(1)求它们的交点A的坐标;
(2)求这两条直线与x轴所围成的三角形面积.
分析 (1)根据两直线相交的问题,通过解方程组$\left\{\begin{array}{l}{y=2x-3}\\{y=6-x}\end{array}\right.$即可得到两直线的交点坐标;
(2)先根据x轴上点的坐标特征求出两直线与x轴的交点坐标,然后根据三角形面积公式求解.
解答 解:(1)解方程组$\left\{\begin{array}{l}{y=2x-3}\\{y=6-x}\end{array}\right.$得$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$,
所以两直线的交点坐标为(3,3);
(2)当y=0时,2x-3=0,解得x=$\frac{3}{2}$,则直线y1=2x-3与x轴的交点坐标为($\frac{3}{2}$,0);
当y=0时,6-x=0,解得x=6,则直线y2=6-x与x轴的交点坐标为(0,6);
所以这两条直线与x轴所围成的三角形面积=$\frac{1}{2}$×(6-$\frac{3}{2}$)×3=$\frac{27}{4}$.
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么它们的自变量系数相同,即k值相同.

练习册系列答案
相关题目
4.不等式组$\left\{\begin{array}{l}{2x+1≥0}\\{x-1<0}\end{array}\right.$的解集是( )
| A. | x≥-$\frac{1}{2}$ | B. | x<1 | C. | -$\frac{1}{2}$≤x<1 | D. | -$\frac{1}{2}$<x<1 |
5.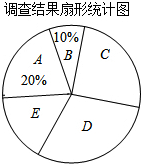 去年以来,我国中东部地区持续出现雾霾天气.我市某记者为了了解“雾霾天气的主要成因”,随机调查了部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计表:
去年以来,我国中东部地区持续出现雾霾天气.我市某记者为了了解“雾霾天气的主要成因”,随机调查了部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计表:
请根据图表中提供的信息解答下列问题:
(1)填空:m=60,n=150,扇形统计图中E组所占百分比为15%;
(2)若该市人口约有75万人,请你估计其中持D组“观点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人持C组“观点”的概率是多少?
 去年以来,我国中东部地区持续出现雾霾天气.我市某记者为了了解“雾霾天气的主要成因”,随机调查了部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计表:
去年以来,我国中东部地区持续出现雾霾天气.我市某记者为了了解“雾霾天气的主要成因”,随机调查了部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计表:| 组别 | 观点 | 频数 |
| A | 大气气压低,空气不流动 | 120 |
| B | 地面灰尘多,空气湿度低 | M |
| C | 汽车尾气排放 | N |
| D | 工厂造成的污染 | 180 |
| E | 其它 | 90 |
(1)填空:m=60,n=150,扇形统计图中E组所占百分比为15%;
(2)若该市人口约有75万人,请你估计其中持D组“观点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人持C组“观点”的概率是多少?
19.下列式子正确的是( )
| A. | ($\sqrt{-2}$)2=2 | B. | $\sqrt{(-5)^{2}}$=-5 | C. | $\sqrt{(-6)^{2}}$=6 | D. | (3$\sqrt{2}$)2=6 |
6.-3的相反数是( )
| A. | 3 | B. | -3 | C. | 0 | D. | ±3 |
 已知函数y=-2x+6与函数y=3x-4.
已知函数y=-2x+6与函数y=3x-4.