题目内容
3．一对质地均匀的正方体骰子的六个面上分别有1到6个点数，将骰子抛掷两次，若两骰子正面点数和为2、10、11、12，则甲赢；如果两骰子正面点数的和为7，则乙赢；若两骰子正面点数的和为其它数，则甲乙都不赢．继续下去，直到有一个人赢为止．你认为游戏对甲、乙是否公平？请说明理由；若不公平，请你修改规则使该游戏对双方公平．分析 列举出所有情况，找到点数和为2、10、11、12的情况数及点数和为7的情况数，求得甲赢的概率和乙赢的概率，若概率相等则公平．
解答 解：表格如下
| （1，6） | （2，6） | （3，6） | （4，6） | （5，6） | （6，6） |
| （1，5） | （2，5） | （3，5） | （4，5） | （5，5） | （6，5） |
| （1，4） | （2，4） | （3，4） | （4，4） | （5，4） | （6，4） |
| （1，3） | （2，3） | （3，3） | （4，3） | （5，3） | （6，3） |
| （1，2） | （2，2） | （3，2） | （4，2） | （5，2） | （6，2） |
| （1，1） | （2，1） | （3，1） | （4，1） | （5，1） | （6，1） |
$\frac{1}{6}$＜$\frac{7}{36}$，
则游戏不公平，甲赢的概率比乙大，
掷一次骰子，向上一面的点数为偶数为甲赢，为奇数为乙赢．
点评 考查用列表格的方法解决游戏公平性问题；用到的知识点为：概率等于所求情况数与总情况数之比；概率大的赢的机会也大．
练习册系列答案
相关题目
13．已知点P1（a-1，4）和P2（2，b）关于x轴对称，则（a+b）2015的值为（ ）
| A． | 72014 | B． | 1 | C． | -1 | D． | （-3）2014 |
“十字相乘法”能把二次三项式分解因式，对于形如ax2+bxy+cy2的x，y二次三项式来说，方法的关键是把x2项系数a分解成两个因数a1，a2的积，即a=a1•a2，把y2项系数c分解成两个因数，c1，c2的积，即c=c1•c2，并使a1•c2+a2•c1正好等于xy项的系数b，那么可以直接写成结果：ax2+bxy+cy2=（a1x+c1y）（a2x+c2y）
如图所示的几何体是由一些小立方块搭成的，则这个几何体的主视图是（ ）
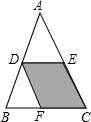如图，在△ABC中，D、E分别是边AB、AC的中点，连接DE，将△ADE沿AB方向平移到△DBF的位置，点D在BC上，已知△ADE的面积为1，则四边形CEDF的面积是2．
13．-（-2）-2=（ ）
| A． | -4 | B． | 4 | C． | -$\frac{1}{4}$ | D． | $\frac{1}{4}$ |