题目内容
 如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOC=60°,点A在第一象限,过点A的双曲线为y=
如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOC=60°,点A在第一象限,过点A的双曲线为y=| k |
| x |
(1)当点O′与点A重合时,t的值是
4
4
;(2)当B′落在双曲线上时,t的值是
2
| 5 |
2
.| 5 |
分析:(1)根据轴对称变换的性质得到当点O′与点A重合时,直线l垂直平分OA,则PA=PB,由B(2,0),∠AOB=60°,根据含30度的直角三角形三边的关系得到AB=
OB=2
,然后由P点坐标为(t,0),则PA=PB=t,PB=t-2,在Rt△PAB中利用勾股定理得到t2=(t-2)2+(2
)2,求出t的值;
(2)连接BB′,B′P,作B′D⊥x轴于点D,由图形反折变换的性质可知直线l是线段BB′的垂直平分线,所以BP=B′P,再由OA⊥l可知OA∥BB′,所以∠B′BP=∠AOB=60°,故B′D是线段BP的垂直平分线,由待定系数法求出直线OA的解析式,故可得出直线BB′的解析式,由此可得出B′点的坐标,进而可得出t的值.
| 3 |
| 3 |
| 3 |
(2)连接BB′,B′P,作B′D⊥x轴于点D,由图形反折变换的性质可知直线l是线段BB′的垂直平分线,所以BP=B′P,再由OA⊥l可知OA∥BB′,所以∠B′BP=∠AOB=60°,故B′D是线段BP的垂直平分线,由待定系数法求出直线OA的解析式,故可得出直线BB′的解析式,由此可得出B′点的坐标,进而可得出t的值.
解答: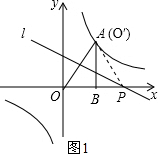 解:(1)点O′与点A重合时,直线l垂直平分OA,如图1,
解:(1)点O′与点A重合时,直线l垂直平分OA,如图1,
连PA,则PA=PO,
∵B(2,0),∠AOB=60°,
∴OB=2,
∴AB=
OB=2
,
∵P点坐标为(t,0),则PA=PO=t,PB=t-2,
在Rt△PAB中,PA2=PB2+AB2,即t2=(t-2)2+(2
)2,解得t=4,
故答案为:4;
(2)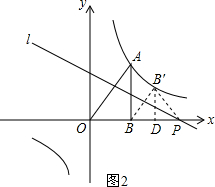 连接BB′,B′P,作B′D⊥x轴于点D,
连接BB′,B′P,作B′D⊥x轴于点D,
∵点B于点B′重合,
∴直线l是线段BB′的垂直平分线,
∴BP=B′P,
∵OA⊥l,
∴OA∥BB′,
∴∠B′BP=∠AOB=60°,
∴B′D是线段BP的垂直平分线,
设直线OA的解析式为y=kx(k≠0),
∵OB=2,AB=2
,
∴A(2,2
),
∴2k=2
,即k=
,
∴直线OA的解析式为y=
x,
∵点A在反比例函数的图象上,
∴反比例函数的解析式为:y=
①.
∵B(2,0),
∴直线BB′的解析式为:y=
x-2
②,
①②联立得,
,
∴B′(1+
,
-
),
∴BD=1+
-2=
-1,
∴BP=2BD=2
-2,
∴OP=BP+OB=2
,
∴P(2
,0),即t=2
.
故答案为:2
.
 解:(1)点O′与点A重合时,直线l垂直平分OA,如图1,
解:(1)点O′与点A重合时,直线l垂直平分OA,如图1,连PA,则PA=PO,
∵B(2,0),∠AOB=60°,
∴OB=2,
∴AB=
| 3 |
| 3 |
∵P点坐标为(t,0),则PA=PO=t,PB=t-2,
在Rt△PAB中,PA2=PB2+AB2,即t2=(t-2)2+(2
| 3 |
故答案为:4;
(2)
 连接BB′,B′P,作B′D⊥x轴于点D,
连接BB′,B′P,作B′D⊥x轴于点D,∵点B于点B′重合,
∴直线l是线段BB′的垂直平分线,
∴BP=B′P,
∵OA⊥l,
∴OA∥BB′,
∴∠B′BP=∠AOB=60°,
∴B′D是线段BP的垂直平分线,
设直线OA的解析式为y=kx(k≠0),
∵OB=2,AB=2
| 3 |
∴A(2,2
| 3 |
∴2k=2
| 3 |
| 3 |
∴直线OA的解析式为y=
| 3 |
∵点A在反比例函数的图象上,
∴反比例函数的解析式为:y=
4
| ||
| x |
∵B(2,0),
∴直线BB′的解析式为:y=
| 3 |
| 3 |
①②联立得,
|
∴B′(1+
| 5 |
| 15 |
| 3 |
∴BD=1+
| 5 |
| 5 |
∴BP=2BD=2
| 5 |
∴OP=BP+OB=2
| 5 |
∴P(2
| 5 |
| 5 |
故答案为:2
| 5 |
点评:本题考查的是反比例函数综合题,涉及到图形反折变换的性质、反比例函数图象上点的坐标特点即用待定系数法求一次函数的解析式等知识,难度适中.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为
如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为 如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为
如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为 (2012•潮阳区模拟)如图,将一块直角三角板ABC和半圆形量角器按图中方式叠放,其中∠A=30°,半圆O的直径MN与直线AC重叠,且切AB于点E,交BC于点F,若测得OM=6cm,∠AOF=120°,求图中阴影部分的面积.(结果可保留π)
(2012•潮阳区模拟)如图,将一块直角三角板ABC和半圆形量角器按图中方式叠放,其中∠A=30°,半圆O的直径MN与直线AC重叠,且切AB于点E,交BC于点F,若测得OM=6cm,∠AOF=120°,求图中阴影部分的面积.(结果可保留π) 如图,将一块直角三角板放置在圆上,使30°角的顶点落在圆上,角的两边与⊙O相交于A、B两点,OA=6cm,则弦AB=
如图,将一块直角三角板放置在圆上,使30°角的顶点落在圆上,角的两边与⊙O相交于A、B两点,OA=6cm,则弦AB=