题目内容
13. 如图,已知△ABC三条边AC=20cm,BC=15cm,AB=25cm,CD⊥AB,则CD=12cm.
如图,已知△ABC三条边AC=20cm,BC=15cm,AB=25cm,CD⊥AB,则CD=12cm.
分析 首先利用勾股定理逆定理证明△ACB是直角三角形,再利用三角形的面积公式可得AC•BC=AB•CD,再代入相应数据进行计算即可.
解答 解:∵202+152=252,
∵AC2+BC2=AB2,
∴△ACB是直角三角形,
∵S△ACB=$\frac{1}{2}•$AC•BC=$\frac{1}{2}$AB•CD,
∴AC•BC=AB•CD,
20×15=25•CD,
CD=12.
故答案为:12.
点评 此题主要考查了勾股定理逆定理,以及直角三角形的面积,关键是掌握如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
3.如图,反映的是某中学九(3)班学生外出方式(乘车、步行、骑车)的频数(人数)分布直方图(部分)和扇形分布图,那么下列说法正确的是( )


| A. | 九(3)班外出的学生共有42人 | |
| B. | 九(3)班外出步行的学生有8人 | |
| C. | 在扇形图中,步行的学生人数所占的圆心角为82 | |
| D. | 如果该校九年级外出的学生共有500人,那么估计全年级外出骑车的学生约有140人 |
1.关于x的方程$\frac{n}{x-1}+\frac{m}{x-2}=0$可能产生的增根是( )
| A. | x=1 | B. | x=2 | C. | x=1或x=2 | D. | x=一1或=2 |

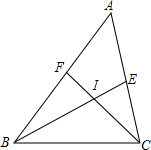 如图,△ABC中,∠ABC和∠ACB的角平分线相交于点I,爱动脑筋的小明同学在写作业时,发现了如下规律:
如图,△ABC中,∠ABC和∠ACB的角平分线相交于点I,爱动脑筋的小明同学在写作业时,发现了如下规律: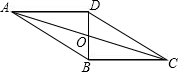 如图,四边形ABCD是平行四边形,己知AD=8,AB=10,BD=5,求BC、CD、OB、OA及此平行四边形的面积.
如图,四边形ABCD是平行四边形,己知AD=8,AB=10,BD=5,求BC、CD、OB、OA及此平行四边形的面积.