题目内容
11.若方程组$\left\{\begin{array}{l}{3x+y=k+1}\\{x+3y=3}\end{array}\right.$的解为x、y,且x+y<0,则一次函数y=kx-k的图象不经过第三象限.分析 方程组$\left\{\begin{array}{l}{3x+y=k+1}\\{x+3y=3}\end{array}\right.$的解为x、y,且x+y<0,则$\frac{1}{4}$k+1<0,求出k的取值,进而求解即可.
解答 解:由方程组$\left\{\begin{array}{l}{3x+y=k+1}\\{x+3y=3}\end{array}\right.$可知x+y=$\frac{1}{4}$k+1,
∵x+y<0,
∴$\frac{1}{4}$k+1<0,
解得k<-4
∴y=kx-k经过第一、二、四象限,不经过第三象限.
故答案为三.
点评 本题考查了一次函数与二元一次方程组的关系,一次函数图象与系数的关系,求出k的值是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
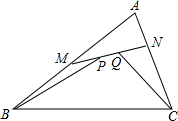 如图,设M、N分别为△ABC的边AB、AC上的点,P、Q为MN上的两点,且MP=QN,求证:MB+CN≤BP+CQ.
如图,设M、N分别为△ABC的边AB、AC上的点,P、Q为MN上的两点,且MP=QN,求证:MB+CN≤BP+CQ.