题目内容
1.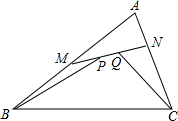 如图,设M、N分别为△ABC的边AB、AC上的点,P、Q为MN上的两点,且MP=QN,求证:MB+CN≤BP+CQ.
如图,设M、N分别为△ABC的边AB、AC上的点,P、Q为MN上的两点,且MP=QN,求证:MB+CN≤BP+CQ.
分析 过点P作PC′∥NC,PC′=NC,连接MC′,证明△MPC′≌△QNC,得到PC′=NC,MC′=QC,利用三角形两边之和大于第三边,得到BO+OM>BM①,PO+OC′>PC′②,①+②得:BO+OM+PO+OC′>BM+PC′,即BP+QC>BM+NC,所以MB+CN≤BP+CQ成立.
解答 解:过点P作PC′∥NC,PC′=NC,连接MC′,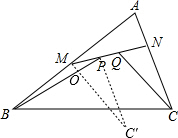
∵PC′∥NC,
∴∠MPC′=∠QNC,
在△MPC′和△QNC中,
$\left\{\begin{array}{l}{MP=QN}\\{∠MPC′=∠QNC}\\{PC′=NC}\end{array}\right.$,
∴△MPC′≌△QNC,
∴PC′=NC,MC′=QC,
在△BOM中,BO+OM>BM,①
在△PC′O中,PO+OC′>PC′,②
①+②得:BO+OM+PO+OC′>BM+PC′,
即BO+PO+OM+OC′>BM+NC,
BP+MC′>BM+NC
BP+QC>BM+NC,
即MB+CN≤BP+CQ成立.
点评 本题考查了全等三角形的性质与判定,三角形的两边之和大于第三边,解决本题的关键是作出辅助线,证明△MPC′≌△QNC.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
12.下列函数中,y是x的二次函数的为( )
| A. | y=-3x2 | B. | y=2x | C. | y=x+1 | D. | y=x3 |
9.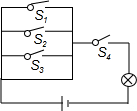 如图所示,是物理课上李老师让小刘同学连接的电路图,现要求:随机同时闭合开关S1、S2、S3、S4中的两个算一次操作,则小刘同学操作一次就能使灯泡?发光的概率是( )
如图所示,是物理课上李老师让小刘同学连接的电路图,现要求:随机同时闭合开关S1、S2、S3、S4中的两个算一次操作,则小刘同学操作一次就能使灯泡?发光的概率是( )
 如图所示,是物理课上李老师让小刘同学连接的电路图,现要求:随机同时闭合开关S1、S2、S3、S4中的两个算一次操作,则小刘同学操作一次就能使灯泡?发光的概率是( )
如图所示,是物理课上李老师让小刘同学连接的电路图,现要求:随机同时闭合开关S1、S2、S3、S4中的两个算一次操作,则小刘同学操作一次就能使灯泡?发光的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
16.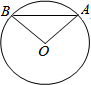 如图,∠AOB=110°,弦AB所对的圆周角为( )
如图,∠AOB=110°,弦AB所对的圆周角为( )
 如图,∠AOB=110°,弦AB所对的圆周角为( )
如图,∠AOB=110°,弦AB所对的圆周角为( )| A. | 55° | B. | 55°或70° | C. | 55°或125° | D. | 55°或110° |