题目内容
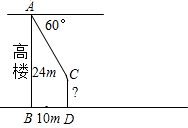如图，王师傅在楼顶上A点处测得楼前一棵树CD的顶端C的俯角为60°，若水平距离BD=10m，楼高AB=24m，则树CD高约为（ ）| A、5m | B、6m | C、7m | D、8m |
考点：解直角三角形的应用-仰角俯角问题
专题：计算题
分析：过C作CE⊥AB，交AB于点E，在直角三角形ACE中，利用30度所对的直角边等于斜边的一半求出AC的长，再利用勾股定理求出AE的长，由AB-AE求出EB的长，即为CD的长．
解答：
解：过C作CE⊥AB，交AB于点E，
在Rt△ACE中，∠EAC=30°，CE=10m，
∴AC=2CE=20m，AE=
=10
m，
则CD=EB=AB-AE=24-10
≈7m．
故选C
解：过C作CE⊥AB，交AB于点E，在Rt△ACE中，∠EAC=30°，CE=10m，
∴AC=2CE=20m，AE=
| AC2-CE2 |
| 3 |
则CD=EB=AB-AE=24-10
| 3 |
故选C
点评：此题考查了解直角三角形的应用-仰角俯角问题，弄清题中的数据是解本题的关键．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
抛物线y=（x-3）2+5的开口方向，对称轴，顶点坐标分别是（ ）
| A、开口向上；x=-3；（-3，5） |
| B、开口向上；x=3；（3，5） |
| C、开口向下；x=3；（-3，-5） |
| D、开口向下；x=-3；（3，-5） |
一元二次方程x2=-3x的根是（ ）
| A、x=-3 |
| B、x=0 |
| C、x1=0，x2=-3 |
| D、x1=0，x2=3 |
点（2，-3）在平面直角坐标系中所在的象限是（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
下列运算正确的是（ ）
| A、x3•x2=x6 |
| B、x6÷x4=x2 |
| C、（x-y）2=x2-y2 |
| D、（2x2）3=2x6 |
下列运算正确的是（ ）
A、
| ||
| B、（a+b）2=a2+b2 | ||
| C、x6÷x3=x2 | ||
D、
|
如图，在△ABC中，分别以AB、AC、BC为边在BC的同侧作等边△ABE、等边△ACD、等边△BCF．