题目内容
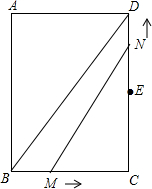 矩形ABCD中,AB=4,tan∠DBC=
矩形ABCD中,AB=4,tan∠DBC=| 4 |
| 3 |
(1)求BC和BD的长;
(2)求运动过程中S与t的函数关系式;
(3)在运动过程中,有时,一个S值,有两个t值与之对应;有时,一个S值,只有一个t值与之对应.请写出“一个S值,只有一个t值与之对应”时,S的取值范围.
考点:四边形综合题
专题:综合题
分析:(1)根据矩形的性质得CD=AB=4,∠BCD=90°,在Rt△BCD中,利用正切的定义可计算出BC=3,然后利用勾股定理可计算出BD=5;
(2)分类讨论:当点N在DE上,即0≤t≤1时,如图1,根据三角形面积公式得到S=-t2+2t+3;
当点N在DB上,即1<t≤3时,如图2,作NH⊥BC于H,则BN=5+2-2t=7-2t,先证明△BNH∽△BDC,利用相似比得到NH=
(7-2t),再根据三角形面积公式得到
S=
t2-
t+
;
(3)当0≤t≤1时,S=-t2+2t+3=-(t-1)2+4,根据二次函数的性质S随t的增大而增大,得到S的范围为3≤S≤4;当1<t≤3时,S=
t2-
t+
,
抛物线的对称轴为直线x=
,根据二次函数的性质S随t的增大而减小,易得S的范围为0≤S<4,于是得到当0≤S<3时,只有一个t值与S对应.
(2)分类讨论:当点N在DE上,即0≤t≤1时,如图1,根据三角形面积公式得到S=-t2+2t+3;
当点N在DB上,即1<t≤3时,如图2,作NH⊥BC于H,则BN=5+2-2t=7-2t,先证明△BNH∽△BDC,利用相似比得到NH=
| 4 |
| 5 |
S=
| 4 |
| 5 |
| 26 |
| 5 |
| 42 |
| 5 |
(3)当0≤t≤1时,S=-t2+2t+3=-(t-1)2+4,根据二次函数的性质S随t的增大而增大,得到S的范围为3≤S≤4;当1<t≤3时,S=
| 4 |
| 5 |
| 26 |
| 5 |
| 42 |
| 5 |
抛物线的对称轴为直线x=
| 13 |
| 4 |
解答: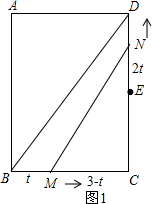 解:(1)∵四边形ABCD为矩形,
解:(1)∵四边形ABCD为矩形,
∴CD=AB=4,∠BCD=90°,
在Rt△BCD中,∵tan∠DBC=
=
,
∴BC=3,
∴BD=
=5;
(2)∵E为CD边的中点,
∴DE=CE=2,
当点N在DE上,即0≤t≤1时,如图1,AM=t,MC=3-t,EN=2t,
∴S=
MC•CN=
(3-t)•(2+2t)=-t2+2t+3;
当点N在DB上,即1<t≤3时,如图2,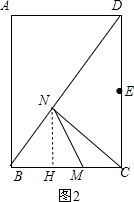 作NH⊥BC于H,则BN=5+2-2t=7-2t,
作NH⊥BC于H,则BN=5+2-2t=7-2t,
∵NH∥BC,
∴△BNH∽△BDC,
∴
=
,即
=
,
∴NH=
(7-2t),
∴S=
MC•NH=
(3-t)•
(7-2t)=
t2-
t+
,
综上所述,S=
;
(3)当0≤t≤1时,S=-t2+2t+3=-(t-1)2+4,
当t=0时,S=3;当t=1时,S=4,
所以S的范围为3≤S≤4;
当1<t≤3时,S=
t2-
t+
,
抛物线的对称轴为直线x=-
=
,
而当t=1时,S=4;当t=3时,S=0,
所以S的范围为0≤S<4,
所以当0≤S<3时,只有一个t值与S对应.
 解:(1)∵四边形ABCD为矩形,
解:(1)∵四边形ABCD为矩形,∴CD=AB=4,∠BCD=90°,
在Rt△BCD中,∵tan∠DBC=
| CD |
| BC |
| 4 |
| 3 |
∴BC=3,
∴BD=
| BC2+CD2 |
(2)∵E为CD边的中点,
∴DE=CE=2,
当点N在DE上,即0≤t≤1时,如图1,AM=t,MC=3-t,EN=2t,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
当点N在DB上,即1<t≤3时,如图2,
 作NH⊥BC于H,则BN=5+2-2t=7-2t,
作NH⊥BC于H,则BN=5+2-2t=7-2t,∵NH∥BC,
∴△BNH∽△BDC,
∴
| NH |
| DC |
| BN |
| BD |
| NH |
| 4 |
| 7-2t |
| 5 |
∴NH=
| 4 |
| 5 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
| 4 |
| 5 |
| 26 |
| 5 |
| 42 |
| 5 |
综上所述,S=
|
(3)当0≤t≤1时,S=-t2+2t+3=-(t-1)2+4,
当t=0时,S=3;当t=1时,S=4,
所以S的范围为3≤S≤4;
当1<t≤3时,S=
| 4 |
| 5 |
| 26 |
| 5 |
| 42 |
| 5 |
抛物线的对称轴为直线x=-
-
| ||
2×
|
| 13 |
| 4 |
而当t=1时,S=4;当t=3时,S=0,
所以S的范围为0≤S<4,
所以当0≤S<3时,只有一个t值与S对应.
点评:本题考查了四边形的综合题:熟练掌握矩形的性质、锐角三角形函数的定义和二次函数的性质;会利用勾股定理和相似比进行几何计算;记住三角形面积公式;
理解分类讨论的思想在数学的应用.
理解分类讨论的思想在数学的应用.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
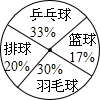 某班学生最喜欢的体育活动如图所示,则下列说法:①最喜欢乒乓球的人数占班级总人数的
某班学生最喜欢的体育活动如图所示,则下列说法:①最喜欢乒乓球的人数占班级总人数的| 33 |
| 100 |
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 17 |
| A、①② | B、①③④ |
| C、②③ | D、①②③ |
已知:m是
的小数部分,则
的值( )
| 2 |
m2+
|
A、等于2
| ||
| B、等于0 | ||
| C、等于2 | ||
| D、随m的变化而变化 |
 如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE. 如图,已知AB=DC,AC=DB.∠1=∠2吗?为什么?
如图,已知AB=DC,AC=DB.∠1=∠2吗?为什么?