题目内容
在坐标原点为0的平面直角坐标系中,直线y=2x+4与y轴交于点A,直线y=-2x-2与x轴交于点B,两直线交于点C,则四边形AOBC的面积为( )
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |
考点:一次函数图象上点的坐标特征
专题:
分析:先求出A、B两点的坐标,再求出C点坐标,连接OC,根据三角形的面积公式即可得出结论.
解答: 解:如图所示:连接OC,
解:如图所示:连接OC,
∵直线y=2x+4与y轴交于点A,
∴A(0,4);
∵直线y=-2x-2与x轴交于点B,
∴B(-1,0).
∵
,解得
,
∴C(-
,1),
∴S四边形AOBC=S△AOC+S△BOC=
×4×
+
×1×1=3+
=
.
故选A.
 解:如图所示:连接OC,
解:如图所示:连接OC,∵直线y=2x+4与y轴交于点A,
∴A(0,4);
∵直线y=-2x-2与x轴交于点B,
∴B(-1,0).
∵
|
|
∴C(-
| 3 |
| 2 |
∴S四边形AOBC=S△AOC+S△BOC=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
故选A.
点评:本题考查的是一次函数图象上点的坐标特点,熟知坐标轴上点的坐标特点是解答此题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
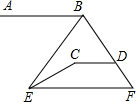 如图,AB∥CD∥EF,∠ABE=50°,∠ECD=160°,则∠BEC的度数为( )
如图,AB∥CD∥EF,∠ABE=50°,∠ECD=160°,则∠BEC的度数为( )| A、20° | B、25° |
| C、30° | D、35° |
 如图,P在∠AOB内,点M、N分别是点P关于AO、BO的对称点,如果△PEF的周长为15,则MN的长为( )
如图,P在∠AOB内,点M、N分别是点P关于AO、BO的对称点,如果△PEF的周长为15,则MN的长为( )| A、15 | B、16 | C、17 | D、18 |
若x<y,则下列各式一定成立的是( )
| A、ax<ay | ||||
| B、-x<-y | ||||
C、
| ||||
| D、x-1<y-1 |
已知反比例函数y=
(k>0)的图象上有两点A(-2,y1),B(2,y2),则y1-y2的值是( )
| k |
| x |
| A、正数 | B、负数 | C、0 | D、无法确定 |
若代数式
有意义,那么x的取值范围是( )
| ||
| x-2 |
| A、x>2 | B、x≥1 |
| C、x≥1且x≠2 | D、x≠2 |
该列数据0,0,1,1,1,2,3的众数是( )
| A、2 | B、0 | C、1 | D、3 |
已知一个样本:26,28,25,29,31,27,30,32,28,26,32,29,28,24,26,27,30,那么下列哪一组的频数为3( )
| A、24.5~26.5 |
| B、26.5~28.5 |
| C、28.5~30.5 |
| D、30.5~32.5 |