题目内容
3．若$\frac{4x-9}{（3x+2）（x-1）}$=$\frac{A}{3x+2}$-$\frac{B}{x-1}$（A、B为常数），则A•B的值为7．分析 通过通分得到分子的对应项，从而求得A、B的值，则易求A•B的值．
解答 解：∵$\frac{A}{3x+2}$-$\frac{B}{x-1}$=$\frac{（x-1）A-（3x+2）B}{（3x+2）（x-1）}$=$\frac{（A-3B）x-（A+2B）}{（3x+2）（x-1）}$，
∴$\frac{4x-9}{（3x+2）（x-1）}$=$\frac{（A-3B）x-（A+2B）}{（3x+2）（x-1）}$，
∴$\left\{\begin{array}{l}{A-3B=4}\\{A+2B=9}\end{array}\right.$，
解得$\left\{\begin{array}{l}{A=7}\\{B=1}\end{array}\right.$，
∴A•B=7×1=7．
故答案是：7．
点评 本题考查了分式的加减法，先通分，然后进行同分母分式加减运算．
练习册系列答案
相关题目
14．已知∠A=30°，则这个角的余角是（ ）
| A． | 30° | B． | 60° | C． | 90° | D． | 150° |
8．若点P（x，-4）与点Q（3，y）关于原点对称，则x-y等于（ ）
| A． | 1 | B． | -1 | C． | -7 | D． | 7 |
15．
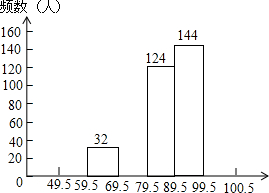某市九年级有15000名学生参加学业水品测试，为了了解本次测试的成绩分布情况，从中抽取了400名学生的得分（得分取正整数，满分100分）进行统计：
频 率 分 布 表
请你根据不完整的频率分布表，解答下列问题：
（1）补全频率分布表和频数分布直方图；
（2）若将得分转化为等级，规定得分低于59.5分评为“D”，59.5～69.5分评为“C”，69.5～89.5分评为“B”，89.5～100.5分评为“A”，这15000名学生中约有多少人为“D”？
某市九年级有15000名学生参加学业水品测试，为了了解本次测试的成绩分布情况，从中抽取了400名学生的得分（得分取正整数，满分100分）进行统计：频 率 分 布 表
| 分 组 | 频 数 | 频 率 |
| 49.5～59.5 | 20 | 0.05 |
| 59.5～69.5 | 32 | 0.08 |
| 69.5～79.5 | 80 | 0.20 |
| 79.5～89.5 | 124 | 0.31 |
| 89.5～100.5 | 144 | 0.36 |
| 合 计 | 400 | 1 |
（1）补全频率分布表和频数分布直方图；
（2）若将得分转化为等级，规定得分低于59.5分评为“D”，59.5～69.5分评为“C”，69.5～89.5分评为“B”，89.5～100.5分评为“A”，这15000名学生中约有多少人为“D”？