Question

8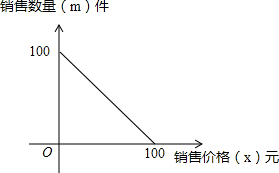．某商场以每件50元的价格购进一种商品，销售中发现这种商品每天的销售量m（件）与每件的销售价x（元）满足一次函数，其图象如图所示．
（1）求出每天的销售数量m（件）与每件的销售价格x（元）的函数解析式；
（2）求该商场每天销售这种商品的销售利润y（元）与每件的销售价格x（元）之间的函数表达式；保证商场赢利并使得每件的售价不超过80元，求出每天商场的最大利润．

Answer 1

分析 （1）设出一次函数的一般表达式m=kx+b，将（0，100）（100，0）代入即可求出；
（2）根据等量关系“销售利润=（销售价格-购进价格）×销售量”列出函数表达式，根据二次函数的顶点式求得最大利润．

解答 解：（1）设出一次函数的一般表达式m=kx+b，将（0，100）（100，0）代入得：
$\left\{\begin{array}{l}{100=b}\\{0=100k+b}\end{array}\right.$，
解得：k=-1，b=100，
故每天的销售数量m（件）与每件的销售价格x（元）的函数解析式为：m=-x+100（0≤x≤100）；

（2）由题意得，y=（x-50）（-x+100）=-x²+150x-5000，
即y=-x²+150x-5000；
∵y=-x²+150x-5000=-（x-75）²+625，
∴当x=75元时，每天商场的最大利润是625元．

点评 本题考查了二次函数的应用，主要利用了待定系数法求一次函数解析式二次函数的关系式的求解，比较简单，根据获利=每件商品的利润×销售量是解题的关键．