题目内容
7.足球世界杯预选赛实行主客场的循环赛,即每两支球队都要在自己的主场和客场踢一场.共举行比赛110场,则参加比赛的球队共有11 支.分析 设参加比赛的球队共有x支,则每支球队都要与余下的(x-1)支球队进行比赛,又每两支球队都要在自己的主场和客场踢一场,即每两支球队相互之间都要比赛两场,故这x支球队一共需要比赛x(x-1)场,而这个场次又是110场,据此列出方程.
解答 解:设参加比赛的球队共有x支,每一个球队都与剩余的x-1队打球,即共打x(x-1)场
∵每两支球队都要在自己的主场和客场踢一场,即每两支球队相互之间都要比赛两场,
∴每两支球队相互之间都要比赛两场,
即x(x-1)=110,
解得:x2-x-110=0,
(x-11)(x+10)=0,
x1=11.x2=-10(负值舍去)
故答案为:11.
点评 此题考查了一元二次方程的应用,解题的关键是抓住“每两支球队都要在自己的主场和客场踢一场”列等量关系.

练习册系列答案
相关题目
18.为了鼓励农民发展生产,国家对购买农机的农户给予农机售价13%的政府补贴,某市农机公司一次性购进A,B两种型号的收割机共30台,根据市场需求,这些收割机可以全部销售.其中,收割机的进价和售价见下表:
设公司计划购进A型收割机x台.
(1)求收割机全部销售后公司获得的利润.(用含x的代数式表示)
(2)当x=10时,求收割机全部销售后公司获得的利润是多少.
| A型收割机 | B型收割机 | |
| 进价(万元/台) | 4 | 3 |
| 售价(万元/台) | 6 | 4 |
(1)求收割机全部销售后公司获得的利润.(用含x的代数式表示)
(2)当x=10时,求收割机全部销售后公司获得的利润是多少.
2. 如图,一只蚂蚁沿边长为1的正方体表面从点A爬到点B,则它走过的路程最短为( )
如图,一只蚂蚁沿边长为1的正方体表面从点A爬到点B,则它走过的路程最短为( )
 如图,一只蚂蚁沿边长为1的正方体表面从点A爬到点B,则它走过的路程最短为( )
如图,一只蚂蚁沿边长为1的正方体表面从点A爬到点B,则它走过的路程最短为( )| A. | $\sqrt{3}$ | B. | 5 | C. | 3 | D. | $\sqrt{5}$ |
16.下列说法:①121的算术平方根是11;②-$\frac{1}{27}$的立方根是-$\frac{1}{3}$;③-81的平方根是±9;④实数和数轴上的点一一对应,其中错误的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
17.如图①,在平面直角坐标系中,平行四边形ABCD在第一象限,且AB∥x轴,直线y=-x从原点出发沿x轴正方向平移,被平行四边形ABCD截得的线段EF的长度l与平移的距离m的函数图象如图②,那么平行四边形ABCD的面积为( )
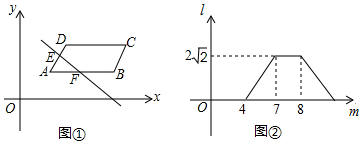

| A. | 4 | B. | $4\sqrt{2}$ | C. | 8 | D. | $8\sqrt{2}$ |

 如图,正方形ABCD内接于⊙O,M为$\widehat{AD}$的中点,连接BM,CM.
如图,正方形ABCD内接于⊙O,M为$\widehat{AD}$的中点,连接BM,CM.