题目内容
13.(1)已知a+$\frac{1}{a}=3,求{a^2}+\frac{1}{a^2}$的值;(2)已知xy=9,x-y=3,求x2+3xy+y2的值.
分析 (1)将$a+\frac{1}{a}=3$两边平方,然后利用完全平方公式进行计算即可;
(2)将x-y=3两边同时平方得:x2-2xy+y2=9,从而可求得x2+y2=27的值,然后将xy=9,x2+y2=27代入所求的代数式即可得出问题的答案.
解答 解:(1)将a+$\frac{1}{a}$=3两边同时平方得:$(a+\frac{1}{a})^{2}=9$,
∴${a}^{2}+2+\frac{1}{{a}^{2}}$=9.
∴${a}^{2}+\frac{1}{{a}^{2}}$=7;
(2)将x-y=3两边同时平方得:x2-2xy+y2=9,
∴x2+y2=9+2xy=9+2×9=27.
∴x2+3xy+y2=27+3×9=54.
点评 本题主要考查的是完全平方公式的应用,平方法的应用是解题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
4.一个直角三角形有两条边分别是3cm、4cm,则第三条边的长度是( )
| A. | 5cm | B. | $\sqrt{7}$cm | C. | 5cm或$\sqrt{7}$cm | D. | 以上都不对 |
2.已知四边形ABCD的四条边分别是a、b、c、d.其中a、c是对边,且a2+b2+c2+d2=2ac+2bd,则四边形一定是( )
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
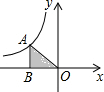 如图,点A在反比例函数y=$\frac{k}{x}$的图象上,AB垂直x轴于点B.若S△AOB=4,则这个反比例函数的解析式为y=-$\frac{8}{x}$.
如图,点A在反比例函数y=$\frac{k}{x}$的图象上,AB垂直x轴于点B.若S△AOB=4,则这个反比例函数的解析式为y=-$\frac{8}{x}$. ”可以得到美丽的“中国结”图案,左边四个图案是由“
”可以得到美丽的“中国结”图案,左边四个图案是由“