题目内容
 如图,在形状和大小不确定的△ABC中,BC=8,E、F分别是AB、AC的中点,P在EF或EF的延长线上,BP交CE于D,Q在CE上且BQ平分∠CBP,设BP=y,PE=x.当CQ=
如图,在形状和大小不确定的△ABC中,BC=8,E、F分别是AB、AC的中点,P在EF或EF的延长线上,BP交CE于D,Q在CE上且BQ平分∠CBP,设BP=y,PE=x.当CQ=| 1 |
| n |
考点:相似三角形的判定与性质
专题:
分析:延长BQ交EF于K,利用平行线及角平分线得出PB=PK,再利用△EQK∽△CQB,得出
=
,利用比例式即可求出y与x之间的函数关系式.
| EK |
| BC |
| EQ |
| CQ |
解答:解:如图,延长BQ交EF于K,

∵EK∥BC,
∴∠EKB=∠KBC,
又∵BQ为∠CBP的平分线,
∴∠PBK=∠KBC,
∴∠EKB=∠PBK,
∴PB=PK=y.
∵CQ=
CE,
∴EQ=(1-
)CE,
∵E,F为AB、AC的中点,
∴∠KEQ=∠BCQ,∠EKQ=∠CBQ,
∴△EQK∽△CQB,
∴
=
,即
=
,
解得y=8(n-1)-x.
故答案为:y=8(n-1)-x.

∵EK∥BC,
∴∠EKB=∠KBC,
又∵BQ为∠CBP的平分线,
∴∠PBK=∠KBC,
∴∠EKB=∠PBK,
∴PB=PK=y.
∵CQ=
| 1 |
| n |
∴EQ=(1-
| 1 |
| n |
∵E,F为AB、AC的中点,
∴∠KEQ=∠BCQ,∠EKQ=∠CBQ,
∴△EQK∽△CQB,
∴
| EK |
| BC |
| EQ |
| CQ |
| x+y |
| 8 |
(1-
| ||
|
解得y=8(n-1)-x.
故答案为:y=8(n-1)-x.
点评:本题主要考查了相似三角形的判定与性质,解题的关键是正确作出辅助线,证出PK=PB.

练习册系列答案
相关题目

 如图,已知反比例函数y=
如图,已知反比例函数y=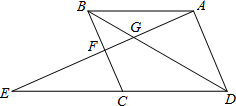 如图,点E为平行四边形ABCD中DC延长线上的一点,且CE=DC.连结AE,分别交BC、BD于点F、G.若BD=6,求DG的长.
如图,点E为平行四边形ABCD中DC延长线上的一点,且CE=DC.连结AE,分别交BC、BD于点F、G.若BD=6,求DG的长. 如图,周长为a的圆上有仅一点A在数轴上,点A所表示的数为1.该圆沿着数轴向右滚动一周后A对应的点为B,且滚动中恰好经过3个整数点(不包括A、B两点),则a的取值范围为
如图,周长为a的圆上有仅一点A在数轴上,点A所表示的数为1.该圆沿着数轴向右滚动一周后A对应的点为B,且滚动中恰好经过3个整数点(不包括A、B两点),则a的取值范围为