题目内容
19.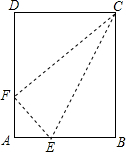 将一张矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB=4,BC=5,则CE的长是$\frac{{5\sqrt{5}}}{2}$.
将一张矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB=4,BC=5,则CE的长是$\frac{{5\sqrt{5}}}{2}$.
分析 要求CE的长,只要求出BE,应先设AE的长为x,根据折叠的性质可得Rt△CBE≌Rt△CFE,所以CF=5,EF=BE=4-x;在Rt△DCF中由勾股定理得:CD2+DF2=CF2,已知CD、CF的长可求出DF的长,又AF=AD-DF=5-DF,在Rt△EAF中由勾股定理可得:EF2=AE2+AF2,求出CE的长,在Rt△CBE中由勾股定理可求出CE.
解答 解:∵四边形ABCD是矩形,
∴AD=BC=5,CD=AB=4,
根据题意得:Rt△CBE≌Rt△CFE,
∴∠CFE=90°,CF=5,EF=BE,
设AE=x,则BE=EF=AB-AE=(4-x),
在Rt△CDF中由勾股定理得:CD2+DF2=CF2,
即42+DF2=102,
∴DF=3,
∴AF=AD-DF=5-3=2,
在Rt△EAF中由勾股定理可得:EF2=AE2+AF2,
即(4-x)2=x2+22,
∴16-8x+x2=x2+4,
∴x=$\frac{3}{2}$,
即CE=$\frac{3}{2}$,
∴BE=$\frac{5}{2}$,
在Rt△CBE中由勾股定理得,
CE=$\sqrt{B{C}^{2}+B{E}^{2}}$=$\sqrt{{5}^{2+}(\frac{5}{2})^{2}}$=$\frac{{5\sqrt{5}}}{2}$.
故答案为:$\frac{{5\sqrt{5}}}{2}$.
点评 本题主要考查了图形的翻折变换以及勾股定理、全等三角形、方程思想等知识,关键是熟练掌握勾股定理,找准对应边.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列问题中,不适宜采用全面调查的是( )
| A. | 调查某校七(1)班同学的体重情况 | |
| B. | 调查我省中小学生的视力情况 | |
| C. | 调查某校七(2)班同学其中考试的语文成绩情况 | |
| D. | 调查某中学全体教师的家庭收入情况 |
4.a2(a2-1)-a2+1的值( )
| A. | 不是负数 | B. | 恒为正数 | C. | 恒为负数 | D. | 不等于0 |
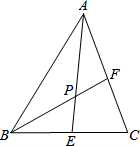 △ABC中,∠ABC=60°,AE、BF是角平分线,且AE、BF交于点P,若AB=6,AP=3PE,则AC长为$\frac{21}{4}$.
△ABC中,∠ABC=60°,AE、BF是角平分线,且AE、BF交于点P,若AB=6,AP=3PE,则AC长为$\frac{21}{4}$.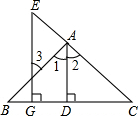 如图,已知AD⊥BC于D,EG⊥BC于G,且∠E=∠3,试说明AD平分∠BAC.
如图,已知AD⊥BC于D,EG⊥BC于G,且∠E=∠3,试说明AD平分∠BAC.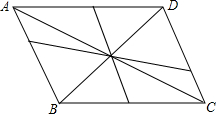 如图,直线BD可以将平行四边形ABCD分成全等的两部分,这样的直线还有很多.
如图,直线BD可以将平行四边形ABCD分成全等的两部分,这样的直线还有很多. 反比例函数y=$\frac{k-1}{x}$如图,则:
反比例函数y=$\frac{k-1}{x}$如图,则: