题目内容
7.两条直线y=k1x+b1和y=k2x+b2相交于点A(3,4),则方程组$\left\{\begin{array}{l}{y={k}_{1}x+{b}_{1}}\\{y={k}_{2}x+{b}_{2}}\end{array}\right.$的解是( )| A. | $\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-3}\\{y=-4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$ |
分析 两个一次函数组成的二元一次方程组的解就是两函数图象的交点坐标.
解答 解:∵直线y=k1x+b1和y=k2x+b2相交于点A(3,4),
∴方程组$\left\{\begin{array}{l}{y={k}_{1}x+{b}_{1}}\\{y={k}_{2}x+{b}_{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$,
故选:B.
点评 此题主要考查了一次函数与二元一次方程组,关键是掌握二元一次方程可以化成一次函数.

练习册系列答案
相关题目
15.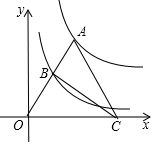 如图,点A为函数y=$\frac{16}{x}$(x>0)图象上一点,连接OA,交函数y=$\frac{4}{x}$(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为( )
如图,点A为函数y=$\frac{16}{x}$(x>0)图象上一点,连接OA,交函数y=$\frac{4}{x}$(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为( )
 如图,点A为函数y=$\frac{16}{x}$(x>0)图象上一点,连接OA,交函数y=$\frac{4}{x}$(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为( )
如图,点A为函数y=$\frac{16}{x}$(x>0)图象上一点,连接OA,交函数y=$\frac{4}{x}$(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
12.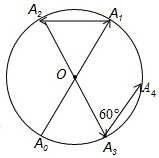 如图所示,一动点从半径为2的⊙O上的A0点出发,沿着射线A0O方向运动到⊙O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到⊙O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处;…按此规律运动到点A2017处,则点A2017与点A0间的距离是( )
如图所示,一动点从半径为2的⊙O上的A0点出发,沿着射线A0O方向运动到⊙O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到⊙O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处;…按此规律运动到点A2017处,则点A2017与点A0间的距离是( )
 如图所示,一动点从半径为2的⊙O上的A0点出发,沿着射线A0O方向运动到⊙O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到⊙O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处;…按此规律运动到点A2017处,则点A2017与点A0间的距离是( )
如图所示,一动点从半径为2的⊙O上的A0点出发,沿着射线A0O方向运动到⊙O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到⊙O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处;…按此规律运动到点A2017处,则点A2017与点A0间的距离是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 2 | D. | 0 |
16.下列各选项中的数是无理数的是( )
| A. | -$\frac{1}{2}$ | B. | 0 | C. | 2 | D. | $\sqrt{5}$ |