题目内容
2．
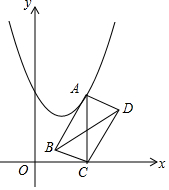如图，在平面直角坐标系中，点A在抛物线y=x2-2x+3上运动，过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为2．
分析 利用配方法求出抛物线的顶点坐标，根据矩形的性质解答．
解答 解：y=x2-2x+3=（x-1）2+2，
则抛物线的顶点坐标为（1，2），
∴当点A在抛物线的顶点时，AC最小，最小值为2，
∵四边形ABCD是矩形，
∴AC=BD，
∴对角线BD的最小值为2，
故答案为：2．
点评 本题考查的是二次函数图象上点的坐标特征、矩形的性质，正确求出抛物线的顶点坐标、掌握矩形的对角线相等是解题的关键．
练习册系列答案
相关题目
12．
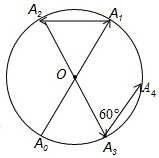如图所示，一动点从半径为2的⊙O上的A0点出发，沿着射线A0O方向运动到⊙O上的点A1处，再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处；接着又从A2点出发，沿着射线A2O方向运动到⊙O上的点A3处，再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处；…按此规律运动到点A2017处，则点A2017与点A0间的距离是（ ）
如图所示，一动点从半径为2的⊙O上的A0点出发，沿着射线A0O方向运动到⊙O上的点A1处，再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处；接着又从A2点出发，沿着射线A2O方向运动到⊙O上的点A3处，再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处；…按此规律运动到点A2017处，则点A2017与点A0间的距离是（ ）| A． | 4 | B． | 2$\sqrt{3}$ | C． | 2 | D． | 0 |
13．
如图，AB∥CD，∠1=50°，∠2的度数是（ ）
如图，AB∥CD，∠1=50°，∠2的度数是（ ）| A． | 50° | B． | 100° | C． | 130° | D． | 140° |
如图，将边长为3cm的等边三角形ABC沿边BC向右平移2cm得到三角形A′B′C′，则四边形AA′C′B的周长是13cm．
7．
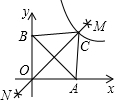如图，点A、B的坐标分别为（2，0）、（0，2），分别以A、B为圆心，大于$\frac{1}{2}$AB的长为半径画弧，两弧相交于点M，N，作直线MN，交函数y=$\frac{k}{x}$（k＞4）的图象于点C，则△ABC的面积为（ ）
如图，点A、B的坐标分别为（2，0）、（0，2），分别以A、B为圆心，大于$\frac{1}{2}$AB的长为半径画弧，两弧相交于点M，N，作直线MN，交函数y=$\frac{k}{x}$（k＞4）的图象于点C，则△ABC的面积为（ ）| A． | k | B． | $\sqrt{k}$ | C． | k-2 | D． | 2$\sqrt{k}$-2 |
11．下列计算正确的是（ ）
| A． | a3+a3=a6 | B． | （a2）3÷a4=a2 | C． | a5•a2=a10 | D． | a7÷a4•a2=a |
12．
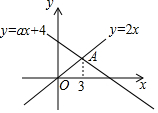如图，函数y=2x和y=ax+4的图象相交于点A（3，m），则不等式2x≥ax+4的解集为（ ）
如图，函数y=2x和y=ax+4的图象相交于点A（3，m），则不等式2x≥ax+4的解集为（ ）| A． | x≥$\frac{3}{2}$ | B． | x≥3 | C． | x$≤\frac{3}{2}$ | D． | x≤3 |