题目内容
有五张卡片,背面颜色,形状,大小完全相同,正面分别写有-1,0,1,2,3,将它们洗匀背面朝上,随机抽一张卡,将正面写的数作为点P的横坐标,再将剩下卡片中任取一张,将正面写的数为点P的纵坐标,则点P落在直线y=x+2和y=-x+6与x轴围成的三角形内的概率是 .
考点:列表法与树状图法,一次函数图象上点的坐标特征
专题:
分析:利用树状图法即可列举出所有可能的结果,然后利用概率公式求解.
解答:解:

共有20种情况,落在直线y=x+2和y=-x+6与x轴围成的三角形内有:(0,1),(1,2)(2,1)(2,3),(3,1)(3,2)共6个.
则概率是:
=
.
故答案是:
.

共有20种情况,落在直线y=x+2和y=-x+6与x轴围成的三角形内有:(0,1),(1,2)(2,1)(2,3),(3,1)(3,2)共6个.
则概率是:
| 6 |
| 20 |
| 3 |
| 10 |
故答案是:
| 3 |
| 10 |
点评:此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
相关题目
在实数-
,
,0.333,
,
,-
,0.4848844884…(相邻两个4之间8的个数逐个加1)中,无理数有( )
| 2 |
| 7 |
| 3 | 6 |
| π |
| 2 |
| 3 | 27 |
| 16 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,OA=OB,数轴上点A表示的数为x,则x2-13的立方根是( )
如图,OA=OB,数轴上点A表示的数为x,则x2-13的立方根是( )A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
 如图中的几何体是圆柱沿竖直方向切掉一半后得到的,从上向下看它将看到( )
如图中的几何体是圆柱沿竖直方向切掉一半后得到的,从上向下看它将看到( )A、 |
B、 |
C、 |
D、 |
 在△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转,旋转角为θ(0°<θ<180°),得△A′B′C.E为AC的中点,A′B′中点为P,AC=4cm,则EP的最大值为
在△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转,旋转角为θ(0°<θ<180°),得△A′B′C.E为AC的中点,A′B′中点为P,AC=4cm,则EP的最大值为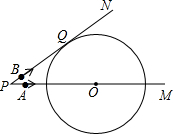 如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动.设运动时间为t s.当t=
如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动.设运动时间为t s.当t= 如图,AB是⊙O的直径,AD、BC和CD分别与⊙O相切于点A、B和E,DA=3.6,CB=6.4,
如图,AB是⊙O的直径,AD、BC和CD分别与⊙O相切于点A、B和E,DA=3.6,CB=6.4,