题目内容
14.证明命题“全等三角形对应边上的高相等”.分析 根据图形写出已知,求证,根据全等三角形的性质求出AB=EF,∠B=∠F,根据全等三角形的判定求出△ABD≌△EFH即可.
解答 解:已知:如图,△ABC≌△EFC,AD、EH分别是△ABC和△EFC的对应边BC、FG上的高.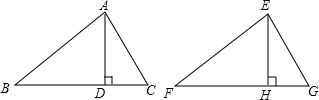
求证:AD=EH.
证明:∵△ABC≌△EFC,
∴AB=EF,∠B=∠F,
∵AD、EH分别是△ABC和△EFC的对应边BC、FG上的高,
∴∠ADB=∠EHF=90°,
在△ABD和△EFH中
$\left\{\begin{array}{l}{∠ADB=∠EHF}\\{∠B=∠F}\\{AB=EF}\end{array}\right.$,
∴△ABD≌△EFH(AAS),
∴AD=EH.
点评 此题主要考查学生对全等三角形的性质及判定的理解及运用能力.注意命题的证明的格式、步骤.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
9.下列命题中,真命题是( )
| A. | 垂直于同一直线的两条直线平行 | |
| B. | 有两边和其中一边上的高对应相等的两个三角形全等 | |
| C. | 三角形三个内角中,至少有2个锐角 | |
| D. | 有两条边和一个角对应相等的两个三角形全等 |
3.科学兴趣小组的同学们,将自己收集的标本向本组的其他成员各赠送一件,全组共互赠了132件,那么全组共有( )名学生.
| A. | 12 | B. | 12或66 | C. | 15 | D. | 33 |