题目内容
15. 如图,在△ABC中,∠ABC=120°,点D、E分别在AC和AB上,且AE=ED=DB=BC,则∠A的度数为15°.
如图,在△ABC中,∠ABC=120°,点D、E分别在AC和AB上,且AE=ED=DB=BC,则∠A的度数为15°.
分析 首先设∠A=x°,由AE=ED=DB=BC,根据等角对等边与三角形外角的性质,可表示出∠C的度数,然后由三角形内角和定理,得到方程120+x+3x=180,解此方程即可求得答案.
解答 解:设∠A=x°,
∵AE=ED,
∴∠ADE=∠A=x°,
∴∠BED=∠A+∠ADE=2x°,
∵ED=DB,
∴∠ABD=∠BED=2x°,
∴∠BDC=∠A+∠ABD=3x°,
∵DB=BC,
∴∠C=∠BDC=3x°,
∵∠ABC+∠A+∠C=180°,∠ABC=120°,
∴120+x+3x=180,
解得:x=15,
∴∠A=15°.
点评 此题考查了等腰三角形的性质以及三角形外角的性质.注意设∠A=x°,利用性质列出方程120+x+3x=180是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.下列美丽的图案中,是中心对称图形的个数是( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.将一些半径相同的小圆按如图所示的规律摆放: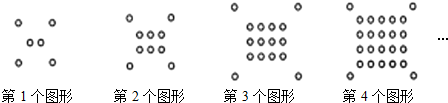
(1)填写下表:
(2)照这样的规律搭下去,搭第8个这样的图形需要76个小圆.

(1)填写下表:
| 图形序号 | 1 | 2 | 3 | 4 | 5 |
| 小圆个数 | 6 | 10 | 16 | 24 | 34 |
10.x10不可能写出如下式子( )
| A. | x2•x4•(x2)2 | B. | (x3)3•x | C. | (-x)3•(-x)5•(-x)2 | D. | (x5)5 |
5.将一个圆分割成三个扇形,它们的圆心角的度数比为1:2:3,则这三个扇形的圆心角的度数分别是( )
| A. | 30°,60°,90° | B. | 60°,120°,180° | C. | 40°,80°,120° | D. | 50°,100°,150° |