题目内容
13.计算:(1)2+$\frac{3}{4}$-($\frac{3}{8}$+4-$\frac{1}{4}$)
(2)-2$\frac{2}{3}$×(-$\frac{1}{4}$)+$\frac{5}{9}$÷(-1$\frac{2}{3}$)
(3)$\frac{2}{3}$×(-9)-36×($\frac{5}{9}$-$\frac{3}{4}$+$\frac{1}{12}$)
(4)(-2)3×(-$\frac{1}{2}$)2+(-$\frac{3}{2}$)2÷(-$\frac{3}{4}$)
分析 (1)首先计算小括号里面的运算,然后从左向右依次计算,求出算式的值是多少即可.
(2)首先计算乘法和除法,然后计算加法,求出算式的值是多少即可.
(3)应用乘法分配律,求出算式的值是多少即可.
(4)首先计算乘方,然后计算乘除法和加法,求出算式的值是多少即可.
解答 解:(1)2+$\frac{3}{4}$-($\frac{3}{8}$+4-$\frac{1}{4}$)
=2$\frac{3}{4}$-4$\frac{1}{8}$
=-1$\frac{3}{8}$
(2)-2$\frac{2}{3}$×(-$\frac{1}{4}$)+$\frac{5}{9}$÷(-1$\frac{2}{3}$)
=$\frac{2}{3}$-$\frac{1}{3}$
=$\frac{1}{3}$
(3)$\frac{2}{3}$×(-9)-36×($\frac{5}{9}$-$\frac{3}{4}$+$\frac{1}{12}$)
=-6-36×$\frac{5}{9}$+36×$\frac{3}{4}$-36×$\frac{1}{12}$
=-6-20+27-3
=-2
(4)(-2)3×(-$\frac{1}{2}$)2+(-$\frac{3}{2}$)2÷(-$\frac{3}{4}$)
=(-8)×$\frac{1}{4}$+$\frac{9}{4}$÷(-$\frac{3}{4}$)
=-2-3
=-5
点评 此题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
1.下列说法中,正确的是( )
| A. | 如果a为有理数,那么-a是负数 | |
| B. | 0和负数称为非负数 | |
| C. | 在数轴上,左边的点所表示的数比右边的点所表示的数大 | |
| D. | 正分数大于负分数 |
8.下列叙述错误的是( )
| A. | 经过两点有一条直线,并且只有一条直线 | |
| B. | 在同一平面内不相交的两条直线叫做平行线 | |
| C. | 连接两点的线段的长,叫做这两点间的距离 | |
| D. | 从直线外一点到这条直线的垂线段,叫做点到直线的距离 |
18.下列说法正确的是( )
| A. | 方程$\sqrt{x}$=4的根是x=±16 | |
| B. | 方程$\sqrt{2x+3}$=x的根是x1=3,x2=-1 | |
| C. | 方程$\sqrt{2x-1}$=x+1变形所得的有理方程是2x-1=x2+1 | |
| D. | 方程$\sqrt{x+1}$+1=0没有实数解 |
5.为提高饮水质量,越来越多的居民选购家用净水器,某商场利用这次商机,计划从厂家购进甲、乙两种型号的家用净水器共300台,进价与售价如下表:
(1)设购进甲种型号净水器x台,销售利润为y元,试求出y与x之间的函数关系式;
(2)由于受资金限制,某商场只能用不多于50000元的资金购进这批家用净水器,为了利润的最大化,商场该如何安排进货?并求出最大利润是多少?
| 型号 | 进价(元/台) | 售价(元/台) |
| A | 150 | 200 |
| B | 200 | 300 |
(2)由于受资金限制,某商场只能用不多于50000元的资金购进这批家用净水器,为了利润的最大化,商场该如何安排进货?并求出最大利润是多少?
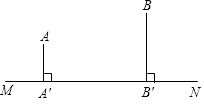 高速公路的同一侧有A,B两城镇,如图所示,它们到高速公路所在直线MN的距离分别为AA′=2km,BB′=4km,且A′B′=8km,要在高速公路上A′,B′之间建一个出口P,使A,B两城镇到P的距离之和最短,求这个最短距离.
高速公路的同一侧有A,B两城镇,如图所示,它们到高速公路所在直线MN的距离分别为AA′=2km,BB′=4km,且A′B′=8km,要在高速公路上A′,B′之间建一个出口P,使A,B两城镇到P的距离之和最短,求这个最短距离.