题目内容
7.若顺次连接四边形各边的中点所得四边形是矩形,则原四边形一定是( )| A. | 梯形 | B. | 对角线相等的四边形 | ||
| C. | 平行四边形 | D. | 对角线互相垂直的四边形 |
分析 此题要根据矩形的性质和三角形中位线定理求解;首先根据三角形中位线定理知:所得四边形的对边都平行且相等,那么其必为平行四边形,若所得四边形是矩形,那么邻边互相垂直,故原四边形的对角线必互相垂直,由此得解.
解答 解:已知:如右图,四边形EFGH是矩形,且E、F、G、H分别是AB、BC、CD、AD的中点,求证:四边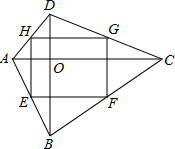 形ABCD是对角线垂直的四边形.
形ABCD是对角线垂直的四边形.
证明:由于E、F、G、H分别是AB、BC、CD、AD的中点,
根据三角形中位线定理得:EH∥FG∥BD,EF∥AC∥HG;
∵四边形EFGH是矩形,即EF⊥FG,
∴AC⊥BD,
故选:D.
点评 本题主要考查了矩形的性质和三角形中位线定理,解题的关键是构造三角形利用三角形的中位线定理解答.

练习册系列答案
相关题目
2.下列图案是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.若5x=2,5y=$\frac{1}{2}$,则x,y之间的关系为( )
| A. | x,y互为相反数 | B. | x,y互为倒数 | C. | x=y | D. | 无法判断 |
19.不等式2(x-2)≤x-2的正整数解的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.对于同一平面内的三条直线a,b,c,下列命题中不正确的是( )
| A. | 若a∥b,b∥c,则a∥c | B. | 若a⊥b,a⊥c,则b⊥c | C. | 若a∥b,a⊥c,则b⊥c | D. | 若a⊥b,a⊥c,则b∥c |
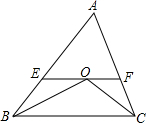 如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于E.交AC于F,若BE=3,CF=2,则EF的长为5.
如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于E.交AC于F,若BE=3,CF=2,则EF的长为5. 如图,CD是线段AB上两点,若CB=4cm,DB=7cm,且D是AC中点,则AC的长等于6cm.
如图,CD是线段AB上两点,若CB=4cm,DB=7cm,且D是AC中点,则AC的长等于6cm.