题目内容
20.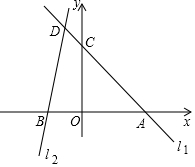 如图,在平面直角坐标系xOy中,直线l1:y=-x+a与x轴交于点A(4,0),与y轴交于点C,直线l2与l1相交于点D(-1,n),与x轴相交于点B(-2,0)
如图,在平面直角坐标系xOy中,直线l1:y=-x+a与x轴交于点A(4,0),与y轴交于点C,直线l2与l1相交于点D(-1,n),与x轴相交于点B(-2,0)(1)求直线l1,l2的解析式;
(2)求四边形OCDB的面积;
(3)设点M是直线l2的一点,且点M的横坐标为m,求△ADM的面积S与m之间的关系式.
分析 (1)根据点A的坐标利用一次函数图象上点的坐标特征,即可求出a的值,进而可得出直线l1的解析式,由点D在直线l1上,可求出点D的坐标,根据点A、D的坐标,利用待定系数法即可求出直线l2的解析式;
(2)利用一次函数图象上点的坐标特征可求出点C的坐标,根据三角形的面积结合S四边形OCDB=S△ABD-S△AOC,即可求出结论;
(3)分m≤-2、-2<m<-1和m≥-1三段,找出S关于m的函数关系式,此题得解.
解答 解:(1)∵直线l1:y=-x+a与x轴交于点A(4,0),
∴0=-4+a,a=4,
∴直线l1的解析式为y=-x+4.
当x=-1时,n=-1×(-1)+4=5,
∴点D的坐标为(-1,5).
设直线l2的解析式为y=kx+b,
将B(-2,0)、D(-1,5)代入y=kx+b,
$\left\{\begin{array}{l}{-2k+b=0}\\{-k+b=5}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=5}\\{b=10}\end{array}\right.$,
∴直线l2的解析式为y=5x+10.
(2)当x=0时,y=-x+4=4,
∴点C的坐标为(0,4).
S四边形OCDB=S△ABD-S△AOC=$\frac{1}{2}$×[4-(-2)]×5-$\frac{1}{2}$×4×4=7.
(3)当x=m时,y=5x+10=5m+10,
∴点M的坐标为(m,5m+10).
分三种情况考虑:


①当m≤-2时,如图1所示.
S=S△ABD+S△ABM=15+$\frac{1}{2}$×6×(-5m-10)=-15m-15;
②当-2<m<-1时,如图2所示.
S=S△ABD-S△ABM=15-$\frac{1}{2}$×6×(5m+10)=-15m-15;
③当m≥-1时,如图3所示.
S=S△ABM-S△ABD=$\frac{1}{2}$×6×(5m+10)-15=15m+15.
综上所述:S=$\left\{\begin{array}{l}{-15m-15(m<-1)}\\{15m+15(m≥-1)}\end{array}\right.$.
点评 本题考查了两条直线相交或平行问题、一次函数图象上点的坐标特征、待定系数法求一次函数解析式以及三角形的面积,解题的关键是:(1)根据点的坐标,利用待定系数法求出直线的解析式;(2)根据三角形的面积结合S四边形OCDB=S△ABD-S△AOC,求出四边形OCDB的面积;(3)分m≤-2、-2<m<-1和m≥-1三段,找出S关于m的函数关系式.

| A. | -x2+3x | B. | -2x2+3x-1 | C. | -2x2+3x+1 | D. | 2x2-3x+1 |
 如图所示,该几何体的左视图是( )
如图所示,该几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
| A. | 2$\sqrt{3}$+3$\sqrt{3}$=5$\sqrt{6}$ | B. | ($\sqrt{2}+1$)(1-$\sqrt{2}$)=1 | C. | (xy)-1($\frac{1}{2}$xy)2=$\frac{1}{4}$xy | D. | -(-a)4÷a2=a2 |
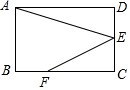 如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF.若AB=2,AD=3,则cos∠AEF的值是$\frac{\sqrt{2}}{2}$.
如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF.若AB=2,AD=3,则cos∠AEF的值是$\frac{\sqrt{2}}{2}$.