Question

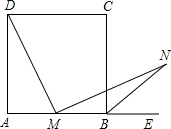如图所示，在正方形ABCD中，M为AB上任意一点，MN丄DM，BN平分∠CBE，试说明：MD=MN．

Answer 1

考点：正方形的性质,全等三角形的判定与性质

专题：证明题

分析：在AD上取一点P，使DP=BM，连接PM，利用正方形的性，证得△MPD≌△NBM，得出结论．

解答：解：在AD上取一点P，使DP=BM，连接PM，
∵四边形ABCD是正方形，
∴AB=AD；
∴AM=AP；
∴∠AMP=∠APM=45°；
∴∠DPM=135°；
而BN平分∠CBE，
∴∠NBE=45°；
∴∠MBN=135°；
∵MN⊥MD，
∴∠ADM+∠AMD=∠NMB+∠AMD=90°，
∴∠ADM=∠NMB，即∠MDP=∠NMB．
在△MPD与△NBM中，

∠DPM=∠MBN PD=BM ∠MDP=∠NMB

，
∴△MPD≌△NBM（ASA），
∴MD=MN．

点评：此题考查正方形的性质，三角形全等的判定；把正方形和全等三角形的知识结合起来，巧妙作出辅助线解决问题．