题目内容
 如图,?ABCD的两条对角线AC,BD相交于点0,AB=
如图,?ABCD的两条对角线AC,BD相交于点0,AB=| 5 |
求证:
(1)AC⊥BD;
(2)?ABCD是菱形.
考点:菱形的判定,平行四边形的性质
专题:证明题
分析:(1)根据AB=
,AO=2,OB=1利用勾股定理的逆定理可判断出△AOB的形状,证得AC⊥BD;
(2)再根据对角线互相垂直的平行四边形是菱形即可判定.
| 5 |
(2)再根据对角线互相垂直的平行四边形是菱形即可判定.
解答:解:(1)?ABCD的两条对角线AC、BD相交于点O,AB=
,AO=2,OB=1,
∵(
)2=22+12,即AB2=OA2+OB2,
∴△AOB是直角三角形,
∴AC⊥BD;
(2)∵四边形ABCD是平行四边形,AC⊥BD,
∴四边形ABCD是菱形.
| 5 |
∵(
| 5 |
∴△AOB是直角三角形,
∴AC⊥BD;
(2)∵四边形ABCD是平行四边形,AC⊥BD,
∴四边形ABCD是菱形.
点评:本题考查的是勾股定理的逆定理、平行四边形及菱形的判定定理,根据勾股定理的逆定理判断出△AOB的形状是解答此题的关键.

练习册系列答案
相关题目
 若两条平行线被第三条直线所截,一组内错角的平分线互相平行.如图,已知AB∥CD,MN平分∠BMH,GH平分∠CHM,求证:MN∥GH.
若两条平行线被第三条直线所截,一组内错角的平分线互相平行.如图,已知AB∥CD,MN平分∠BMH,GH平分∠CHM,求证:MN∥GH.
 如图所示,在一个凹型图形中,下列说法都正确吗?如果不正确,请加以更正.
如图所示,在一个凹型图形中,下列说法都正确吗?如果不正确,请加以更正.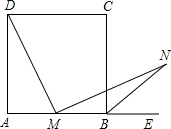 如图所示,在正方形ABCD中,M为AB上任意一点,MN丄DM,BN平分∠CBE,试说明:MD=MN.
如图所示,在正方形ABCD中,M为AB上任意一点,MN丄DM,BN平分∠CBE,试说明:MD=MN. 如图,AB∥CD,AD∥BC,若∠CBE=68°,则∠C=
如图,AB∥CD,AD∥BC,若∠CBE=68°,则∠C=